
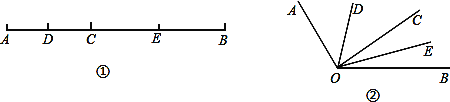
【题目】如图①,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若AC=4cm,求DE的长;
(2)试利用“字母代替数”的方法,说明不论AC取何值(不超过12cm),DE的长不变;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
【答案】(1)DE=6cm;(2)见解析;(3)见解析.
【解析】试题分析:(1)由AC=4cm,AB=12cm,即可推出BC=8cm,然后根据点D、E分别是AC和BC的中点,即可推出AD=DC,BE=EC,由此即可得到DE的长度;
(2)设AC=acm,然后通过点D、E分别是AC和BC的中点,即可推出DE=CD+CE=![]() (AC+BC)=
(AC+BC)= ![]() AB,由此即可得到结论;
AB,由此即可得到结论;
(3)由若OD、OE分别平分∠AOC和∠BOC,即可推出∠DOE=∠DOC+∠COE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)= ![]() ∠AOB,继而可得到答案.
∠AOB,继而可得到答案.
试题解析:(1)∵AB=12cm,
∴AC=4cm,
∴BC=8cm,
∵点D、E分别是AC和BC的中点,
∴CD=2cm,CE=4cm,
∴DE=6cm,
(2)设AC=acm,
∵点D、E分别是AC和BC的中点,
∴DE=CD+CE=![]() (AC+BC)=
(AC+BC)=![]() AB=6cm,
AB=6cm,
∴不论AC取何值(不超过12cm),DE的长不变,
(3)∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOE=∠DOC+∠COE=![]() (∠AOC+∠COB)=
(∠AOC+∠COB)=![]() ∠AOB,
∠AOB,
∵∠AOB=120°,
∴∠DOE=60°,
∴∠DOE的度数与射线OC的位置无关.


科目:初中数学 来源: 题型:
【题目】阅读下面材料并回答问题:
点A,B在数轴上分别表示数a,b,A,B两点之间的距离表示为AB.
当A,B两点中有一点在原点时:
不妨设A在原点,如图1,AB=OB=|b|=|a-b|;
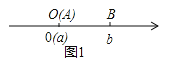
当A,B两点都不在原点时:
①如图2,点A,B都在原点的右边,AB=OB-OA=|b|-|a|=b-a=|a-b|;
![]()
②如图3,点A,B都在原点左边,AB=OB-OA=|b|-|a|=(-b)-(-a)=|a-b|;

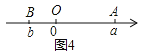
③如图4,点A,B在原点的两边,AB=OA+OB=|a|+|b|=a+(-b)=|a-b|;
综上,数轴上A,B两点之间的距离AB=|a-b|.
(1)回答问题:数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ,数轴上表示x和-1的两点之间的距离是 .
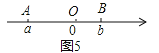
(2)如图5,若|a-b|=2013,且OA=2OB,求a+b的值.
(3)结合两点之间的距离,若点M表示的数为x,当代数式|x+1|+|x-2|取最小值时,相应x的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( ) 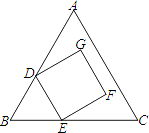
A.2
B.3
C.12﹣4 ![]()
D.6 ![]() ﹣6
﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD. 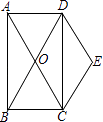
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过A(3,0)、B(4,1)两点,且与y轴交于点C.
经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
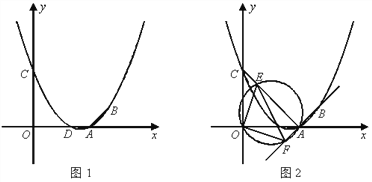
(2)如图1,设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值;
(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,则小聪最多可以买几支钢笔?设小聪购买x支钢笔,则可列关于x的一元一次不等式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF为( ) 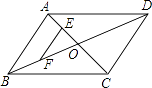
A.3厘米
B.4厘米
C.5厘米
D.6厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com