
【题目】如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( ) 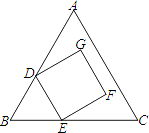
A.2
B.3
C.12﹣4 ![]()
D.6 ![]() ﹣6
﹣6
【答案】D
【解析】解:如图,过点B作BH⊥AC于H,交GF于K, 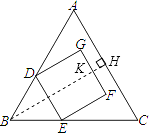
∵△ABC是等边三角形,
∴∠A=∠ABC=60°,
∵BD=BE,
∴△BDE是等边三角形,
∴∠BDE=60°,
∴∠A=∠BDE,
∴AC∥DE,
∵四边形DEFG是正方形,GF=6,
∴DE∥GF,
∴AC∥DE∥GF,
∴KH=18× ![]() ﹣6×
﹣6× ![]() ﹣6=9
﹣6=9 ![]() ﹣3
﹣3 ![]() ﹣6=6
﹣6=6 ![]() ﹣6,
﹣6,
∴F点到AC的距离为6 ![]() ﹣6.
﹣6.
故选D.
【考点精析】根据题目的已知条件,利用等边三角形的性质和正方形的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
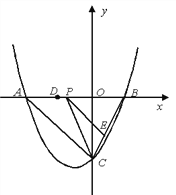
【题目】如图,抛物线y=![]() x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
(1)求该抛物线的解析式;
(2) 若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3) 若点D为OA的中点,点M是线段AC上一点,且△OMD是等腰三角形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面的点阵图形和与之对应的等式,探究其中的规律:
(1) 请你在④和⑤后面的横线上分别写出对应的等式:
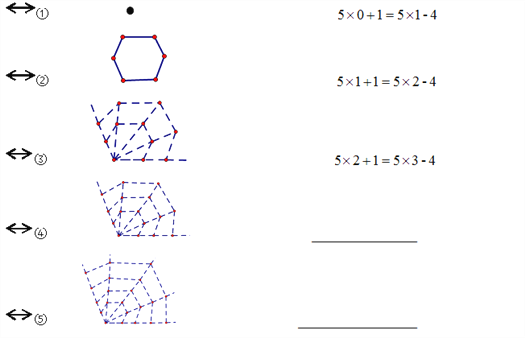
(2)通过猜想,写出与第n个点阵图形相对应的等式.
(3)求:点的个数等于96的点阵图形是第几个.
(4)判断:是否存在点的个数等于2018的点阵图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN. 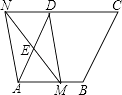
(1)求证:四边形AMDN是平行四边形;
(2)当AM=时,四边形AMDN是矩形(直接写答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3方格上做填字游戏,要求每行每列及对角线上三个方格中的数字和都等于S,又填在图中三格中的数字如图,若要能填成,则( )
10
8 13
A.S=24 B.S=30 C.S=31 D.S=39
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益Z(元)会相应降低且Z与x之间也大致满足如图②所示的一次函数关系.
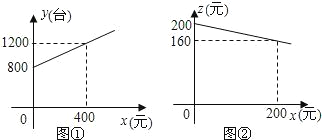
(1)在政府未出台补贴措施前,该商场销售彩电的总收益额为多少元?
(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;
(3)要使该商场销售彩电的总收益w(元)最大,政府应将每台补贴款额x定为多少并求出总收益w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
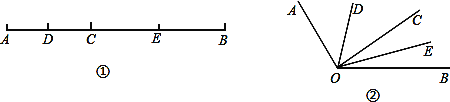
【题目】如图①,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若AC=4cm,求DE的长;
(2)试利用“字母代替数”的方法,说明不论AC取何值(不超过12cm),DE的长不变;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
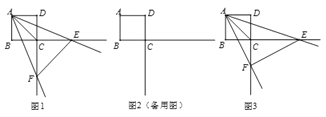
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF。设CE=a,CF=b。
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com