
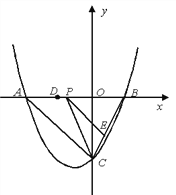
【题目】如图,抛物线y=![]() x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
(1)求该抛物线的解析式;
(2) 若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3) 若点D为OA的中点,点M是线段AC上一点,且△OMD是等腰三角形,求M点的坐标.
【答案】(1)抛物线的解析式为y=![]() x2+x-4;
x2+x-4;
(2)△PCE面积的最大值为3;
(3)M点的坐标为(-1,-3)或(-2,-2).
【解析】试题分析:本题主要考查二次函数的图象与性质、相似三角形的判定与性质以及等腰三角形。
(1)将点A的坐标和点B的坐标代入抛物线的解析式中,即可求得该抛物线的解析式。
(2)将y=0代入抛物线的解析式中,得到点A的坐标,因为PE//AC,所以∠BPE=∠BAC,∠BEP=∠BCA,则△BPE∽△BAC,由相似三角形的面积比等于相似比的平方的性质求得△PCE的面积方程,即可求得△PCE面积的最大值。
(3)根据题意,分类讨论△OMD为等腰三角形的情况,①当OD=DM时,因为点D为OA的中点,所以△ADM为等腰三角形,因为OA=OC,且∠AOC=90,所以△AOC为等腰直角三角形,即可求得点M的坐标。②当DM=OM时,过点M作AB的垂线交于N点,连接MN,因为MN⊥AB,由等腰三角形的性质可知,MN是△OMD的中线,所以ON=DN=1,设为y=kx+b,将点A的坐标和点C的坐标代入上式得直线AC的解析式,则将x=1代入直线AC的解析式中,即可求得点M的坐标。③当DO=OM时,OM最小为点O到AC的距离,因为△AOC为等腰直角三角形,即可证明DO=OM不成立。
试题解析:(1)把点C(0,-4),B(2,0)分别代入y=![]() x2+bx+c中,
x2+bx+c中,
c=-4
![]() ×22+2b+c=0
×22+2b+c=0
∴b=1
∴y=![]() x2+x-4
x2+x-4
(2)设P点坐标为(x,0),则BP=2-x,
∵![]() x2+x-4=0 得x1=2,x2=4
x2+x-4=0 得x1=2,x2=4
∴A点坐标为(-4,0)
∴S△ABC =![]() AB·OC=
AB·OC=![]() ×6×4=12
×6×4=12
∵PE∥AC
∴∠BPE =∠BAC ,∠BEP =∠BCA
∴△BPE∽△BAC…
∴![]() =(
=(![]() )2 即
)2 即![]() =
=![]()
所以S△BPE =![]() (2-x)2
(2-x)2
又∵S△BCP =![]() (2-x) ×4=2(2-x)
(2-x) ×4=2(2-x)
∴ S△PCE =S△BCP -S△BPE =2(2-x)-![]() (2-x)2 =-
(2-x)2 =-![]() x2 -
x2 -![]() x+
x+![]() =-
=-![]() (x+1)2+3
(x+1)2+3
∴x=-1时△PCE面积的最大值是3.
(3)当MO=MD时,过M作MM1⊥OD,垂足为M1,则M1为OD的中点
∴OM1=DM1=1
又∵∠OAC =45°
∴M1M=M1A=3
∴M点的坐标为(-1,-3)
当DM=DO时,
DO=DM=DA=2
∴∠OAC =∠AMD=45°
∴∠ADM =90°
∴M点的坐标为(-2,-2)
当OM=OD时,过O作OM2⊥AC,垂足为M2,
∵OA =4
∴OM2=2![]()
又OM≥OM2=2![]()
又∵OD=2
∴OM>OD
∴在AC上不存在点M,使OM=OD
所以M点的坐标为(-1,-3)或(-2,-2).


科目:初中数学 来源: 题型:
【题目】腰长为x,底边长为y的等腰三角形的周长为12,则y与x的函数表达式为____________,自变量x的取值范围为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年(2)班的同学在募捐活动中,自愿捐款如下:
每人捐款数(元) | 2 | 5 | 10 | 20 |
相应人数 | 5 | 10 | 20 | 15 |
根据表中给的信息回答下列问题:
(1)该班有多少名学生?
(2)全班共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器按成本价提高30%后标价,再打八折销售,售价为2080元.设该电器的成本价为x元,由题意,下面所列方程正确的是( )
A.80%(1+30%)x=2080
B.30%80%x=2080
C.2080×30%×80%=x
D.30%x=2080×80%
查看答案和解析>>
科目:初中数学 来源: 题型:
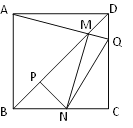
【题目】如图,边长一定的正方形ABCD,Q是CD上一动点,AQ交BD于点M,过M作MN⊥AQ交BC于N点,作NP⊥BD于点P,连接NQ,下列结论:①AM=MN;
②MP=![]() BD;③BN+DQ=NQ;④
BD;③BN+DQ=NQ;④![]() 为定值。其中一定成立的是_______.
为定值。其中一定成立的是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料并回答问题:
点A,B在数轴上分别表示数a,b,A,B两点之间的距离表示为AB.
当A,B两点中有一点在原点时:
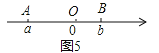
不妨设A在原点,如图1,AB=OB=|b|=|a-b|;
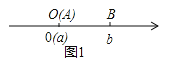
当A,B两点都不在原点时:
①如图2,点A,B都在原点的右边,AB=OB-OA=|b|-|a|=b-a=|a-b|;
![]()
②如图3,点A,B都在原点左边,AB=OB-OA=|b|-|a|=(-b)-(-a)=|a-b|;

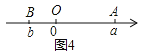
③如图4,点A,B在原点的两边,AB=OA+OB=|a|+|b|=a+(-b)=|a-b|;
综上,数轴上A,B两点之间的距离AB=|a-b|.
(1)回答问题:数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ,数轴上表示x和-1的两点之间的距离是 .
(2)如图5,若|a-b|=2013,且OA=2OB,求a+b的值.
(3)结合两点之间的距离,若点M表示的数为x,当代数式|x+1|+|x-2|取最小值时,相应x的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( ) 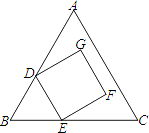
A.2
B.3
C.12﹣4 ![]()
D.6 ![]() ﹣6
﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com