
【题目】阅读下面材料并回答问题:
点A,B在数轴上分别表示数a,b,A,B两点之间的距离表示为AB.
当A,B两点中有一点在原点时:
不妨设A在原点,如图1,AB=OB=|b|=|a-b|;
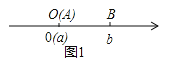
当A,B两点都不在原点时:
①如图2,点A,B都在原点的右边,AB=OB-OA=|b|-|a|=b-a=|a-b|;
![]()
②如图3,点A,B都在原点左边,AB=OB-OA=|b|-|a|=(-b)-(-a)=|a-b|;

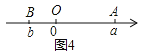
③如图4,点A,B在原点的两边,AB=OA+OB=|a|+|b|=a+(-b)=|a-b|;
综上,数轴上A,B两点之间的距离AB=|a-b|.
(1)回答问题:数轴上表示2和5的两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ,数轴上表示x和-1的两点之间的距离是 .
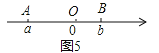
(2)如图5,若|a-b|=2013,且OA=2OB,求a+b的值.
(3)结合两点之间的距离,若点M表示的数为x,当代数式|x+1|+|x-2|取最小值时,相应x的取值范围是
【答案】(1)3,3,4,|x+1|;(2)-671;(3)-1≤x≤2.
【解析】试题分析:(1)根据两点间的距离公式即可求解;
(2)根据题意列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值;
的值;
(3)当![]() 大于等于0,且
大于等于0,且![]() 小于等于0时,原式取得最小值,求出这个最小值即可.
小于等于0时,原式取得最小值,求出这个最小值即可.
试题解析:(1)数轴上表示2和5的两点之间的距离是52=3,数轴上表示2和5的两点之间的距离是2(5)=3,数轴上表示1和3的两点之间的距离是1(3)=4,数轴上表示x和1的两点之间的距离是|x+1|.
(2)∵|ab|=2013,且OA=2OB,
∴3b=2013,解得b=671,
a=2b=1342,
a+b=1342+671=671.
故a+b的值是671.
(3)数形结合,若|x+1|+|x2|取最小值,那么表示x的点M在1和2之间的线段上,
所以![]()
故答案为:3,3,4,|x+1|; ![]()


科目:初中数学 来源: 题型:
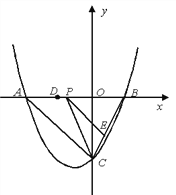
【题目】如图,抛物线y=![]() x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
x2+bx+c与y轴交于点C(0,-4),与x轴交于A、B,且点B的坐标为(2,0).
(1)求该抛物线的解析式;
(2) 若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值;
(3) 若点D为OA的中点,点M是线段AC上一点,且△OMD是等腰三角形,求M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于正比例函数 y 3x ,下列说法正确的是( )
A. y 随 x 的增大而减小 B. y 随 x 的增大而增大
C. y 随 x 的减小而增大 D. y 有最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于多项式22t2+3t﹣1,下列说法中不正确的是( )
A.它是关于t的二次三项式
B.它是按t降幂排列
C.它的常数项是﹣1
D.二次项的系数是2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面的点阵图形和与之对应的等式,探究其中的规律:
(1) 请你在④和⑤后面的横线上分别写出对应的等式:
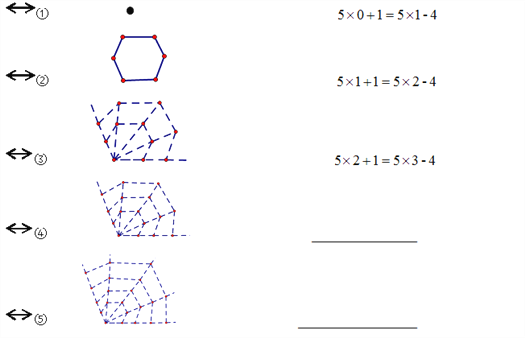
(2)通过猜想,写出与第n个点阵图形相对应的等式.
(3)求:点的个数等于96的点阵图形是第几个.
(4)判断:是否存在点的个数等于2018的点阵图形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN. 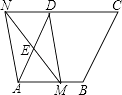
(1)求证:四边形AMDN是平行四边形;
(2)当AM=时,四边形AMDN是矩形(直接写答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若AC=4cm,求DE的长;
(2)试利用“字母代替数”的方法,说明不论AC取何值(不超过12cm),DE的长不变;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
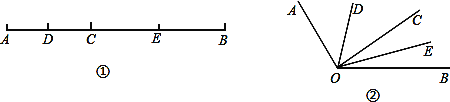
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com