
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD. 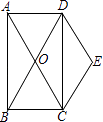
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
【答案】
(1)证明:∵CE∥OD,DE∥OC,
∴四边形OCED是平行四边形,
∵矩形ABCD,∴AC=BD,OC= ![]() AC,OD=
AC,OD= ![]() BD,
BD,
∴OC=OD,
∴四边形OCED是菱形
(2)解:在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=4,
∴BC=2,
∴AB=DC=2 ![]() ,
,
连接OE,交CD于点F,
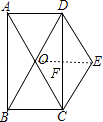
∵四边形ABCD为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF= ![]() BC=1,
BC=1,
∴OE=2OF=2,
∴S菱形OCED= ![]() ×OE×CD=
×OE×CD= ![]() ×2×2
×2×2 ![]() =2
=2 ![]()
【解析】(1)根据平行四边形的判定得出四边形OCED是平行四边形,根据矩形的性质求出OC=OD,根据菱形的判定得出即可.(2)解直角三角形求出BC=2.AB=DC=2 ![]() ,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF=
,连接OE,交CD于点F,根据菱形的性质得出F为CD中点,求出OF= ![]() BC=1,求出OE=2OF=2,求出菱形的面积即可.
BC=1,求出OE=2OF=2,求出菱形的面积即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在3×3方格上做填字游戏,要求每行每列及对角线上三个方格中的数字和都等于S,又填在图中三格中的数字如图,若要能填成,则( )
10
8 13
A.S=24 B.S=30 C.S=31 D.S=39
查看答案和解析>>
科目:初中数学 来源: 题型:
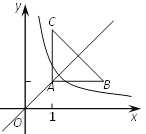
【题目】如图,Rt△ABC在第一象限, ![]() ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线![]() 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥![]() 轴,AC∥
轴,AC∥![]() 轴,若双曲线
轴,若双曲线![]() 与
与![]() 有交点,则k的取值范围是_______.
有交点,则k的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
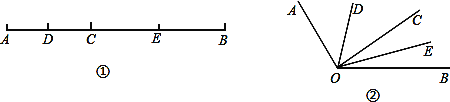
【题目】如图①,已知线段AB=12cm,点C为AB上的一个动点,点D、E分别是AC和BC的中点.
(1)若AC=4cm,求DE的长;
(2)试利用“字母代替数”的方法,说明不论AC取何值(不超过12cm),DE的长不变;
(3)知识迁移:如图②,已知∠AOB=120°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE的度数与射线OC的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图. 根据以上信息,解答下列问题: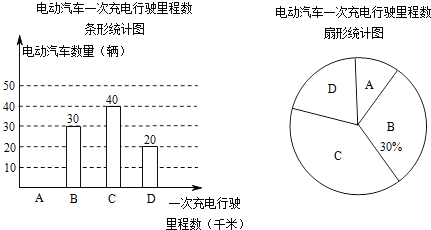
(1)问这次被抽检的电动汽车共有几辆?
(2)补全条形统计图,并求出C等级对应的圆心角度数.
(3)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com