
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
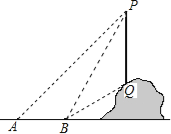
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:![]() ,
,![]() .
.
【答案】(1)30°;(2)9m.
【解析】试题分析:(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
试题解析:延长PQ交直线AB于点E,
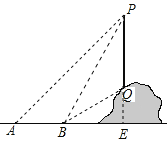
(1)∠BPQ=90°-60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x米,
x米,
∵AB=AE-BE=6米,
则x-![]() x=6,
x=6,
解得:x=9+3![]() .
.
则BE=(3![]() +3)米.
+3)米.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=(3+
+3)=(3+![]() )米.
)米.
∴PQ=PE-QE=9+3![]() -(3+
-(3+![]() )=6+2
)=6+2![]() ≈9(米).
≈9(米).
答:电线杆PQ的高度约9米.


科目:初中数学 来源: 题型:
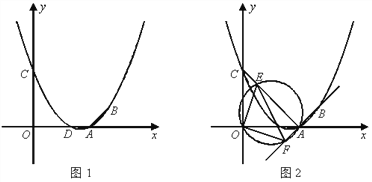
【题目】已知抛物线![]() 经过A(3,0)、B(4,1)两点,且与y轴交于点C.
经过A(3,0)、B(4,1)两点,且与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,设抛物线与x轴的另一个交点为D,在抛物线的对称轴上找一点H,使△CDH的周长最小,求出H点的坐标并求出最小周长值;
(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合),经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求面积的最小值及E点坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF为( ) 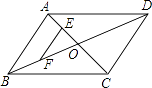
A.3厘米
B.4厘米
C.5厘米
D.6厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①ab是一次单项式;②单项式﹣x2y的系数是﹣1;③3+x2﹣4x是按x的降幂排列的;④数4是单项式;这四句话中不正确的是( )
A.①③
B.②③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将代数式3x2y+5xy2﹣3y3﹣5x3按y的降幂排列是( )
A.﹣5x3+3x2y+5xy2﹣3y3
B.﹣3y3+5xy2+3x2y﹣5x3
C.﹣5x3﹣3y3+3x2y+5xy2
D.3x2y+5xy2﹣3y3﹣5x3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD﹣A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交(其中n是正整数).那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时,它们之间的距离是( ) 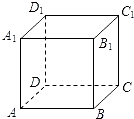
A.0
B.1
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com