
分析 首先根据已知得出$\frac{1}{x}$=$-\frac{\sqrt{5}+1}{2}$,x2+$\frac{1}{{x}^{2}}$=3,将原式化简为$\sqrt{(x-\frac{1}{x}){(x}^{2}+\frac{1}{{x}^{2}}+1)}$,将$\frac{1}{x}$=$-\frac{\sqrt{5}+1}{2}$,x2+$\frac{1}{{x}^{2}}$=3,代入即可.
解答 解:∵x=$\frac{1-\sqrt{5}}{2}$,
∴$\frac{1}{x}$=$-\frac{\sqrt{5}+1}{2}$,x2+$\frac{1}{{x}^{2}}$=3,
∴原式=$\sqrt{(x-\frac{1}{x}){(x}^{2}+\frac{1}{{x}^{2}}+1)}$=$\sqrt{1×(3+1)}$=2,
故答案为:2.
点评 本题主要考查了二次根式的化简求值,将二次根式化简,利用立方差公式是解答此题的关键.


科目:初中数学 来源: 题型:填空题
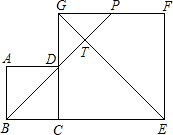 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$.
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT的长为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
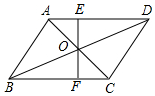 已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.
已知:在?ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则?ABCD的面积是32.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a$\sqrt{x}$-b$\sqrt{y}$ | B. | b$\sqrt{x}$-a$\sqrt{y}$ | C. | $\sqrt{y}$-$\sqrt{x}$ | D. | $\sqrt{y}$+$\sqrt{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24 | B. | 14+2$\sqrt{7}$ | C. | 24或14+2$\sqrt{7}$ | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com