
在平面直角坐标系中,横坐标与纵坐标都为整数的点叫整点,动点P从原点O出发,运动速度为每秒1个单位长度,规定P只能向上或向右运动,请回答下列问题:
(1)填表
运动时间(秒) 可得到的整点坐标 整点个数
t=1
t=2
t=3
(2)当t=12时,整点有 个;
(3)当t= 时,可得到整点(8,7);
(4)当t= 时,可得到整点(m,n).
解:(1)以1秒时达到的整数点为基准,向上或向右移动一格得到2秒时的可能的整数点;
再以2秒时得到的整数点为基准,向上或向右移动一格,得到3秒时可能得到的整数点,
故答案为:
t=1 (0,1)、(1,0) 2
t=2 (0,2)、(2,0)、(1,1) 3
t=3 (0,3)、(3,0)、(2,1)、(1,2) 4
(2)∵1秒时,达到2个整数点;2秒时,达到3个整数点;3秒时,达到4个整数点,
∴t=12秒时,应达到13个整数点,
故答案为13;
(3)横坐标为8,需要从原点开始沿x轴向右移动8秒,纵坐标为7,需再向上移动5秒,所以需要的时间为15秒,
故答案为15;
(4)横坐标为m,需要从原点开始沿x轴向右移动m秒,纵坐标为n,需再向上移动n秒,所以需要的时间为(m+n)秒.
故答案为:(m+n).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
古希腊的毕达哥拉斯学派把1,3,6,10,…称为三角形数;把1,4,9,16,…称为数正方形数.“三角形数”和“正方形数”之间存在如下图所示的关系:
即两个相邻的“三角形数”的和为一个“正方形数”,则下列等式符合以上规律的是( )
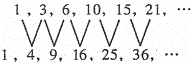
A. 6+15=21 B. 36+45=81 C. 9+16=25 D. 30+34=64
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=( )
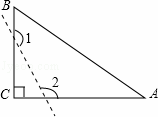
A. 90° B. 135° C. 270° D. 315°
查看答案和解析>>
科目:初中数学 来源: 题型:
我们知道:任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果ax+b=0,其中a、b为有理数,x为无理数,那么a=0且b=0.运用上述知识,解决下列问题:
(1)如果 ,其中a、b为有理数,那么
,其中a、b为有理数,那么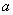 = ,
= , = ;
= ;
(2)如果 ,其中a、b为有理数,求
,其中a、b为有理数,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com