

分析 (1)如图②所示,取AB、BC、CD、DA的中点E、F、G、H连接EF、FG、GH、HE,四边形EFGH是菱形,根据三角形中位线定理即可证明.
(2)①由IJ∥BD,JK∥AC,得$\frac{IJ}{BD}$=$\frac{AJ}{AB}$,$\frac{JK}{AC}$=$\frac{JB}{AB}$,所以$\frac{IJ}{BD}$+$\frac{jk}{AC}$=$\frac{AJ}{AB}$+$\frac{JB}{AB}$=$\frac{AJ+JB}{AB}$=$\frac{AB}{AB}$=1.又IJ=JK,AC=k•BD,所以$\frac{JI}{BD}$+$\frac{JK}{k•BD}$=1,由此即可求出$\frac{IJ}{BD}$的值.
②由$\frac{IJ}{BD}$+$\frac{JK}{AC}$=1,推出$\frac{JK}{AC}$=$\frac{1}{1+k}$,可得S△AIJ=($\frac{k}{1+k}$)2•S△ABD,S△CKL=($\frac{k}{1+k}$)2•S△BDC,S△DIL=($\frac{1}{1+k}$)2•S△ADC,S△BJK=($\frac{1}{1+k}$)2•S△ABC,根据四边形ABCD的面积是四边形IJKL面积的3倍,列出方程即可解决问题.
解答 解:(1)如图②所示,取AB、BC、CD、DA的中点E、F、G、H连接EF、FG、GH、HE,四边形EFGH是菱形.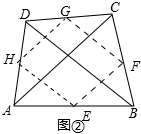
理由:∵AC=BD,AE=EB,AH=HD,CF=FB,CG=DG,
∴EH=GF=$\frac{1}{2}$BD,同理可得HG=EF=$\frac{1}{2}$AC,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
(2)①如图③中,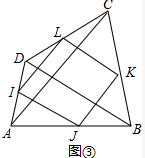
∵IJ∥BD,JK∥AC,
∴$\frac{IJ}{BD}$=$\frac{AJ}{AB}$,$\frac{JK}{AC}$=$\frac{JB}{AB}$,
∴$\frac{IJ}{BD}$+$\frac{jk}{AC}$=$\frac{AJ}{AB}$+$\frac{JB}{AB}$=$\frac{AJ+JB}{AB}$=$\frac{AB}{AB}$=1.
∵IJ=JK,AC=k•BD
∴$\frac{JI}{BD}$+$\frac{JK}{k•BD}$=1,
∴$\frac{k•IJ+JK}{k•BD}$=1,
∴$\frac{IJ}{BD}$=$\frac{k}{1+k}$,
故答案为1.$\frac{k}{1+k}$.
②∵$\frac{IJ}{BD}$+$\frac{JK}{AC}$=1,
∴$\frac{k•IJ}{k•BD}$+$\frac{JK}{AC}$=1,
∴$\frac{JK}{AC}$=$\frac{1}{1+k}$,
∵$\frac{JK}{BD}$=$\frac{KL}{BD}$=$\frac{k}{1+k}$,
∴S△AIJ=($\frac{k}{1+k}$)2•S△ABD,S△CKL=($\frac{k}{1+k}$)2•S△BDC,S△DIL=($\frac{1}{1+k}$)2•S△ADC,S△BJK=($\frac{1}{1+k}$)2•S△ABC,
∵四边形ABCD的面积是四边形IJKL面积的3倍,
∴S四边形ABCD=3[S四边形ABCD-($\frac{k}{1+k}$)2•S四边形ABCD-($\frac{1}{1+k}$)2•S四边形ABCD],
整理得k2-4k+1=0,
解得k=2+$\sqrt{3}$或2-$\sqrt{3}$,
∴AC=k•BD=10+5$\sqrt{3}$后10-5$\sqrt{3}$.
点评 本题考查四边形综合题、三角形中位线定理、平行线分线段成比例定理,相似三角形的性质等知识,解题的关键是灵活运用比例的性质解决问题,学会用转化的思想思考问题,把问题转化为方程解决,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 根据要求完成下面的填空:
根据要求完成下面的填空:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
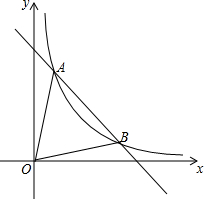 如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y1=-x+5的图象与反比例函数y2=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com