
【题目】如图所示,在平面直角坐标系中,已知一次函数y=![]() x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
x+1的图象与x轴,y轴分别交于A,B两点,以AB为边在第二象限内作正方形ABCD.
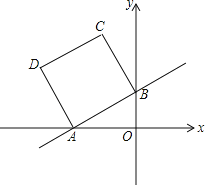
(1)求边AB的长;
(2)求点C,D的坐标;
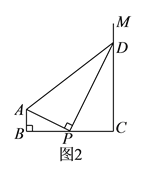
(3)在x轴上是否存在点M,使△MDB的周长最小?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)C(﹣1,3),D(﹣3,2);(3)M(﹣1,0).
;(2)C(﹣1,3),D(﹣3,2);(3)M(﹣1,0).
【解析】
试题分析:(1)在直角三角形AOB中,由OA与OB的长,利用勾股定理求出AB的长即可;
(2)过C作y轴垂线,过D作x轴垂线,分别交于点E,F,可得三角形CBE与三角形ADF与三角形AOB全等,利用全等三角形对应边相等,确定出C与D坐标即可;
(3)作出B关于x轴的对称点B′,连接B′D,与x轴交于点M,连接BD,BM,此时△MDB周长最小,求出此时M的坐标即可.
解:(1)对于直线y=![]() x+1,令x=0,得到y=1;令y=0,得到x=﹣2,
x+1,令x=0,得到y=1;令y=0,得到x=﹣2,
∴A(﹣2,0),B(0,1),
在Rt△AOB中,OA=2,OB=1,
根据勾股定理得:AB=![]() =
=![]() ;
;
(2)作CE⊥y轴,DF⊥x轴,可得∠CEB=∠AFD=∠AOB=90°,
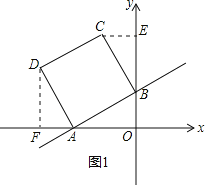
∵正方形ABCD,
∴BC=AB=AD,∠DAB=∠ABC=90°,
∴∠DAF+∠BAO=90°,∠ABO+∠CBE=90°,
∵∠DAF+∠ADF=90°,∠BAO+∠ABO=90°,
∴∠BAO=∠ADF=∠CBE,
∴△BCE≌△DAF≌ABO,
∴BE=DF=OA=2,CE=AF=OB=1,
∴OE=OB+BE=2+1=3,OF=OA+AF=2+1=3,
∴C(﹣1,3),D(﹣3,2);
(3)找出B关于x轴的对称点B′,连接B′D,与x轴交于点M,此时△BMD周长最小,
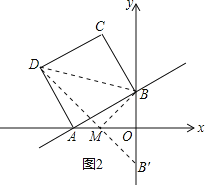
∵B(0,1),
∴B′(0,﹣1),
设直线B′D的解析式为y=kx+b,
把B′与D坐标代入得:![]() ,
,
解得:![]() ,即直线B′D的解析式为y=﹣x﹣1,
,即直线B′D的解析式为y=﹣x﹣1,
令y=0,得到x=﹣1,即M(﹣1,0).


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
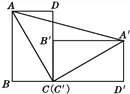
【题目】如图,将竖直放置的长方形砖块ABCD推倒至长方形A'B'C'D'的位置,长方形ABCD的长和宽分别为a,b,AC的长为c.
(1)你能用只含a,b的代数式表示S△ABC,S△C'A'D'和S直角梯形A'D'BA吗?能用只含c的代数式表示S△ACA'吗?
(2)利用(1)的结论,你能验证勾股定理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
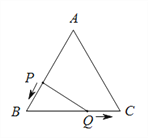
【题目】如图,已知△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1 cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),则(1)BP![]() cm,BQ
cm,BQ![]() cm.(用含t的代数式表示)
cm.(用含t的代数式表示)
(2)当t为何值时,△PBQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象经过点A(-4,0),B(2,6)两点.
(1)求一次函数y=kx+b的表达式;
(2)在直角坐标系中,画出这个函数的图象;
(3)求这个一次函数与坐标轴围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,点E,F,G分别是BD,AC,DC的中点.已知两底之差是6,两腰之和是12,则△EFG的周长是( )
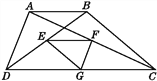
A. 8 B. 9 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
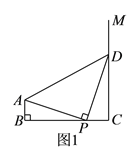
【题目】如图, ![]() ,射线
,射线![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,过点
重合)上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() ,求证:
,求证: ![]() ≌
≌![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() 平分
平分![]() ,试猜测
,试猜测![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() 是等腰三角形,作点
是等腰三角形,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连结
,连结![]() ,则
,则![]() __________.(请直接写出答案)
__________.(请直接写出答案)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com