
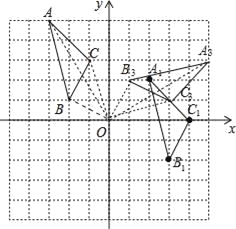
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

【答案】(1)图形见解析;A1的坐标为(2,2),B1点的坐标为(3,﹣2);(2)图形见解析;A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);(3)图形见解析;A3(5,3),B3(1,2),C3(3,1).
【解析】试题分析:(1)利用点C和点C1的坐标变化得到平移的方向与距离,然后利用此平移规律写出顶点A1,B1的坐标;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用网格和旋转的性质画出△A2B3C3,然后写出△A2B3C3的各顶点的坐标.
试题解析:(1)如图,△A1B1C1为所作,
因为点C(﹣1,3)平移后的对应点C1的坐标为(4,0),
所以△ABC先向右平移5个单位,再向下平移3个单位得到△A1B1C1,
所以点A1的坐标为(2,2),B1点的坐标为(3,﹣2);
(2)因为△ABC和△A1B2C2关于原点O成中心对称图形,
所以A2(3,﹣5),B2(2,﹣1),C2(1,﹣3);
(3)如图,△A2B3C3为所作,A3(5,3),B3(1,2),C3(3,1);


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为![]() 、
、![]() 、5(画一个即可).并且直接写出此时三角形DEF的面积.
、5(画一个即可).并且直接写出此时三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:在等腰三角形ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边三角形ACE,直线BE交直线AD于点F,连接FC.
(1)如图1,120°<∠BAC<180°,△ACE与△ABC在直线AC的异侧,且FC交AE于点M.
①求证:∠FEA=∠FCA;
②猜想线段FE,FA,FD之间的数量关系,并证明你的结论:
(2)当60°<∠BAC<120°,且△ACE与△ABC在直线AC的同侧时,利用图2画出图形探究线段FE,FA,FD之间的数量关系,并直接写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,∠ACB=45°,AD、CF都是高,相交于点P,角平分线BE分别交AD、CF于Q、S,则图中的等腰三角形个数是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H,
(1)求证:∠BCE=∠CAD;
(2)直接写出∠CFD的度数;并写出线段AF与线段HF的数量关系.(无需解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需要成本1700元;若购进甲种3株,乙种1株,则共需要成本1500元.
(1)求甲乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲、乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=CB,点E在边BC上,点F在边AB的延长线上,BE=BF. 
(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com