
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпЙ§AЃЈ1ЃЌ0ЃЉЁЂBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉШ§ЕуЃЌжБЯпADНЛХзЮяЯпгкЕуDЃЌЕуDЕФКсзјБъЮЊЉ2ЃЌЕуPЃЈmЃЌnЃЉЪЧЯпЖЮADЩЯЕФЖЏЕуЃЌЙ§ЕуPЕФжБЯпДЙжБгкxжсЃЌНЛХзЮяЯпгкЕуQЃЎ
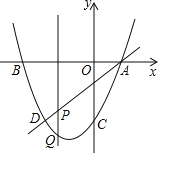
ЃЈ1ЃЉЧѓжБЯпADМАХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЯпЖЮPQЕФГЄЖШlгыmЕФЙиЯЕЪНЃЌmЮЊКЮжЕЪБЃЌPQзюГЄЃП
ЃЈ3ЃЉдкЦНУцФкЪЧЗёДцдкећЕуЃЈКсЁЂзнзјБъЖМЮЊећЪ§ЃЉRЃЌЪЙЕУPЁЂQЁЂDЁЂRЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕуRЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжБЯпADЕФНтЮіЪНЮЊyЃНxЉ1ЃЌХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНx2+2xЉ3ЃЛЃЈ2ЃЉlЃНЉm2Љm+2 ЃЈЉ2ЁмmЁм1ЃЉЃЌЕБmЃНЉ![]() ЪБЃЌPQзюГЄЃЌзюДѓжЕЮЊ
ЪБЃЌPQзюГЄЃЌзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉДцдкЃЌЗћКЯЬѕМўЕФЕуRЙВга6ИіЃЌМДЃКR1ЃЈЉ2ЃЌЉ2ЃЉЃЌR2ЃЈЉ2ЃЌЉ4ЃЉЃЌR3ЃЈЉ2ЃЌЉ1ЃЉЃЌR4ЃЈЉ2ЃЌЉ5ЃЉЃЌR5ЃЈ0ЃЌЉ3ЃЉR6ЃЈ2ЃЌЉ1ЃЉЃЎ
ЃЛЃЈ3ЃЉДцдкЃЌЗћКЯЬѕМўЕФЕуRЙВга6ИіЃЌМДЃКR1ЃЈЉ2ЃЌЉ2ЃЉЃЌR2ЃЈЉ2ЃЌЉ4ЃЉЃЌR3ЃЈЉ2ЃЌЉ1ЃЉЃЌR4ЃЈЉ2ЃЌЉ5ЃЉЃЌR5ЃЈ0ЃЌЉ3ЃЉR6ЃЈ2ЃЌЉ1ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉХзЮяЯпyЃНax2+bxЉ3Й§AЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌДњШыПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЌЕуDдкХзЮяЯпЩЯЧвКсзјБъЮЊЉ2ЃЌПЩЧѓЕуDЕФзјБъЃЌИљОнAЁЂDСНЕузјБъЃЌгУД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпADЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPдкADЩЯЃЌЕуQдкХзЮяЯпЩЯЃЌЕБКсзјБъЮЊmЪБЃЌЯргІЕФзнзјБъПЩвдИљОнНтЮіЪНБэЪОГіРДЃЌЖјPQЕФГЄlОЭЪЧPЕуЁЂQЕузнзјБъЕФВюЃЌгкЪЧПЩвдЕУЕНlгыmЕФКЏЪ§ЙиЯЕЪНЃЌдйвРОнКЏЪ§ЕФзюжЕЃЌПЩЧѓmЮЊКЮжЕЪБЃЌPQзюГЄЃЌPQЕФзюДѓжЕвВФмЧѓГіЃЛ
ЃЈ3ЃЉЪЙPЃЌQЃЌDЃЌRЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌПЩвдЗжСНжжЧщПіЃКвЛЪЧPQЮЊвЛБпЪБЃЌЕуRБидкжБЯпxЃНЉ2ЩЯЃЌдйИљОнPQЮЊзюДѓжЕвдЯТЕФећЪ§жЕЃЌЕУЕНPQЕФећЪ§жЕЃЌдкжБЯпxЃНЉ2ЩЯПЩвдевЕНЕуRЕФЮЛжУЃЌШЗЖЈЕуRЕФзјБъЃЌЕУГідкЕуDЩЯЗНДцдкЃЌдкЕуDЯТЗНвВДцдкЃЛЖўЪЧPQЮЊвЛЬѕЖдНЧЯпЪБЃЌИљОнЦНааЫФБпаЮЕФаджЪЃЌPQгыDRЛЅЯрЦНЗжЃЌДЫЪБRгыC жиКЯЃЎ
НтЃКЃЈ1ЃЉЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНax2+bx+cЃЌНЋAЃЈ1ЃЌ0ЃЉЃЌBЃЈЉ3ЃЌ0ЃЉCЃЈ0ЃЌЉ3ЃЉДњШыyЃНax2+bx+cЕУЃК
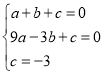 ЃЌ
ЃЌ
НтЕУЃК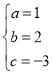 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНx2+2xЉ3ЃЌ
ЕБxЃНЉ2ЪБЃЌyЃНЃЈЉ2ЃЉ2Љ4Љ3ЃНЉ3ЃЌ
ЁрDЃЈЉ2ЃЌЉ3ЃЉЃЌ
ЩшжБЯпADЕФНтЮіЪНЮЊyЃНkx+bЃЌНЋAЃЈ1ЃЌ0ЃЉЃЌDЃЈЉ2ЃЌЉ3ЃЉДњШыЕУЃК
![]()
НтЕУЃК![]() ЃЌ
ЃЌ
ЁржБЯпADЕФНтЮіЪНЮЊyЃНxЉ1ЃЛ
вђДЫжБЯпADЕФНтЮіЪНЮЊyЃНxЉ1ЃЌХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНx2+2xЉ3ЃЎ
ЃЈ2ЃЉЁпЕуPдкжБЯпADЩЯЃЌQХзЮяЯпЩЯЃЌPЃЈmЃЌnЃЉЃЌ
ЁрnЃНmЉ1 QЃЈmЃЌm2+2mЉ3ЃЉ
ЁрPQЕФГЄlЃНЃЈmЉ1ЃЉЉЃЈm2+2mЉ3ЃЉЃНЉm2Љm+2 ЃЈЉ2ЁмmЁм1ЃЉ
ЁрЕБmЃНЉ![]() ЃН
ЃН![]() ЪБЃЌPQЕФГЄlзюДѓЃНЉЃЈЉ
ЪБЃЌPQЕФГЄlзюДѓЃНЉЃЈЉ![]() ЃЉ2ЉЃЈЉ
ЃЉ2ЉЃЈЉ![]() ЃЉ+2ЃН
ЃЉ+2ЃН![]() ЃЎ
ЃЎ
Д№ЃКЯпЖЮPQЕФГЄЖШlгыmЕФЙиЯЕЪНЮЊЃКlЃНЉm2Љm+2 ЃЈЉ2ЁмmЁм1ЃЉ
ЕБmЃНЉ![]() ЪБЃЌPQзюГЄЃЌзюДѓжЕЮЊ
ЪБЃЌPQзюГЄЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉЂйШєPQЮЊЦНааЫФБпаЮЕФвЛБпЃЌдђRвЛЖЈдкжБЯпxЃНЉ2ЩЯЃЌШчЭМЃК
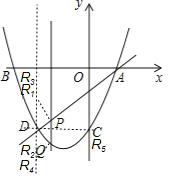
ЁпPQЕФГЄЮЊ0ЃМPQЁм![]() ЕФећЪ§ЃЌ
ЕФећЪ§ЃЌ
ЁрPQЃН1ЛђPQЃН2ЃЌ
ЕБPQЃН1ЪБЃЌдђDRЃН1ЃЌДЫЪБЃЌдкЕуDЩЯЗНгаR1ЃЈЉ2ЃЌЉ2ЃЉЃЌдкЕуDЯТЗНгаR2ЃЈЉ2ЃЌЉ4ЃЉЃЛ
ЕБPQЃН2ЪБЃЌдђDRЃН2ЃЌДЫЪБЃЌдкЕуDЩЯЗНгаR3ЃЈЉ2ЃЌЉ1ЃЉЃЌдкЕуDЯТЗНгаR4ЃЈЉ2ЃЌЉ5ЃЉЃЛ
ЂкШєPQЮЊЦНааЫФБпаЮЕФвЛЬѕЖдНЧЯпЃЌдђPQгыDRЛЅЯрЦНЗжЃЌ
ЕБPQЃН1ЪБЃЌМДЃКxЉ1ЉЃЈx2+2xЉ3ЃЉЃН1ЃЌДЫЪБxВЛЪЧећЪ§ЃЌ
ЕБPQЃН2ЪБЃЌМДxЉ1ЉЃЈx2+2xЉ3ЃЉЃН2ЃЌДЫЪБx1ЃНЉ1ЃЌx2ЃН0ЃЛЕБx1ЃНЉ1ЃЌRгыЕуCжиКЯЃЌМДR5ЃЈ0ЃЌЉ3ЃЉЃЌЕБx2ЃН0ЃЛДЫЪБR6ЃЈ2ЃЌЉ1ЃЉ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуRгаЃКR1ЃЈЉ2ЃЌЉ2ЃЉЃЌR2ЃЈЉ2ЃЌЉ4ЃЉЃЌR3ЃЈЉ2ЃЌЉ1ЃЉЃЌR4ЃЈЉ2ЃЌЉ5ЃЉЃЌR5ЃЈ0ЃЌЉ3ЃЉЃЌ
R6ЃЈ2ЃЌЉ1ЃЉЃЎ
Д№ЃКЗћКЯЬѕМўЕФЕуRЙВга6ИіЃЌМДЃКR1ЃЈЉ2ЃЌЉ2ЃЉЃЌR2ЃЈЉ2ЃЌЉ4ЃЉЃЌR3ЃЈЉ2ЃЌЉ1ЃЉЃЌR4ЃЈЉ2ЃЌЉ5ЃЉЃЌR5ЃЈ0ЃЌЉ3ЃЉR6ЃЈ2ЃЌЉ1ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЗЂЯжЮЪЬтЃЉАЎКУЪ§бЇЕФаЁУїдкзізївЕЪБХіЕНетбљЕФвЛЕРЬтФПЃК
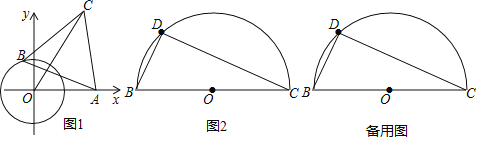
ШчЭМ1ЃЌЕуOЮЊзјБъдЕуЃЌЁбOЕФАыОЖЮЊ1ЃЌЕуAЃЈ2ЃЌ0ЃЉЃЎЖЏЕуBдкЁбOЩЯЃЌСЌНсABЃЌзїЕШБпЁїABCЃЈAЃЌBЃЌCЮЊЫГЪБеыЫГађЃЉЃЌЧѓOCЕФзюДѓжЕЃЎ
ЃЈНтОіЮЪЬтЃЉаЁУїОЙ§ЖрДЮЕФГЂЪдгыЬНЫїЃЌжегкЕУЕННтЬтЫМТЗЃКдкЭМЂйжаЃЌСЌНгOBЃЌвдOBЮЊБпдкOBЕФзѓВрзїЕШБпШ§НЧаЮBOEЃЌСЌНгAEЃЎ
ЃЈ1ЃЉЧыФуевГіЭМжагыOCЯрЕШЕФЯпЖЮЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЧыжБНгаДГіЯпЖЮOCЕФзюДѓжЕЃЎ
ЃЈЧЈвЦЭиеЙЃЉ
ЃЈ3ЃЉШчЭМ2ЃЌBCЃН4![]() ЃЌЕуDЪЧвдBCЮЊжБОЖЕФАыдВЩЯВЛЭЌгкBЁЂCЕФвЛИіЖЏЕуЃЌвдBDЮЊБпзїЕШБпЁїABDЃЌЧыЧѓГіACЕФзюжЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЌЕуDЪЧвдBCЮЊжБОЖЕФАыдВЩЯВЛЭЌгкBЁЂCЕФвЛИіЖЏЕуЃЌвдBDЮЊБпзїЕШБпЁїABDЃЌЧыЧѓГіACЕФзюжЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
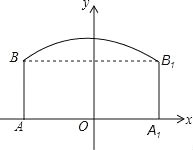
ЁОЬтФПЁПШчЭМЃЌЫэЕРЕФНиУцгЩХзЮяЯпКЭГЄЗНаЮЙЙГЩЃЌГЄЗНаЮЕФГЄЮЊ16mЃЌПэЮЊ6mЃЌХзЮяЯпЕФзюИпЕуCРыЕиУцAA1ЕФОрРыЮЊ8mЃЎ
ЃЈ1ЃЉАДШчЭМЫљЪОЕФжБНЧзјБъЯЕЃЌЧѓБэЪОИУХзЮяЯпЕФКЏЪ§БэДяЪНЃЎ
ЃЈ2ЃЉвЛДѓаЭЦћГЕзАдиФГДѓаЭЩшБИКѓЃЌИпЮЊ7mЃЌПэЮЊ4mЃЌШчЙћИУЫэЕРФкЩшЫЋЯђааГЕЕРЃЌФЧУДетСОДћГЕФмЗёАВШЋЭЈЙ§ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
дкбЇЯАЁЖдВЁЗетвЛеТЪБЃЌРЯЪІИјЭЌбЇУЧВМжУСЫвЛЕРГпЙцзїЭМЬтЃК
ГпЙцзїЭМЃКЙ§дВЭтвЛЕузїдВЕФЧаЯпЃЎ
вбжЊЃКPЮЊЁбOЭтвЛЕуЃЎ
ЧѓзїЃКОЙ§ЕуPЕФЁбOЕФЧаЯпЃЎ
аЁУєЕФзїЗЈШчЯТЃК
ШчЭМЃЌ
ЃЈ1ЃЉСЌНгOPЃЌзїЯпЖЮOPЕФДЙжБЦНЗжЯпMNНЛOPгкЕуCЃЛ
ЃЈ2ЃЉвдЕуCЮЊдВаФЃЌCOЕФГЄЮЊАыОЖзїдВЃЌНЛЁбOгкAЃЌBСНЕуЃЛ
ЃЈ3ЃЉзїжБЯпPAЃЌPBЃЎЫљвджБЯпPAЃЌPBОЭЪЧЫљЧѓзїЕФЧаЯпЃЎ
РЯЪІШЯЮЊаЁУєЕФзїЗЈе§ШЗЃЎ
ЧыЛиД№ЃКСЌНгOAЃЌOBКѓЃЌПЩжЄЁЯOAPЃНЁЯOBPЃН90ЁуЃЌЦфвРОнЪЧ_____ЃЛгЩДЫПЩжЄУїжБЯпPAЃЌPBЖМЪЧЁбOЕФЧаЯпЃЌЦфвРОнЪЧ_____ЃЎ
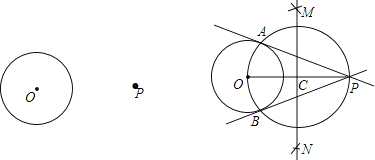
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2+bx+cЃН0ЃЎ
ЃЈ1ЃЉШєbЃН2mЉ1ЃЌm+cЃНЉ6ЃЌХаЖЯЗНГЬИљЕФЧщПіЃЛ
ЃЈ2ЃЉШєЗНГЬгаСНИіЯрЕШЕФЗЧСуЪЕЪ§ИљЃЌЧвb2Љc2Љ4ЃН0ЃЌЧѓДЫЪБЗНГЬЕФИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЁЂDЪЧАыдВABЕФШ§ЕШЗжЕуЃЌЙ§ЕуCзїADбгГЄЯпЕФДЙЯпCEЃЌДЙзуЮЊEЃЎ

ЃЈ1ЃЉЧѓжЄЃКCEЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ2ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЈ3ЃЉШєЯвCNЙ§ЁїABCЕФФкаФЕуMЃЌMNЃН![]() ЃЌЧѓCNЃЎ
ЃЌЧѓCNЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
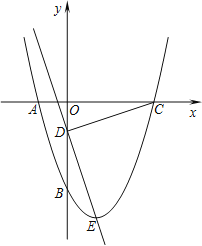
ЁОЬтФПЁПШчЭМЫљЪОЃЌХзЮяЯпy=x2+bx+cОЙ§AЁЂBСНЕуЃЌAЁЂBСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ0ЃЉЁЂЃЈ0ЃЌЉ3ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЕуEЮЊХзЮяЯпЕФЖЅЕуЃЌЕуCЮЊХзЮяЯпгыxжсЕФСэвЛНЛЕуЃЌЕуDЮЊyжсЩЯвЛЕуЃЌЧвDC=DEЃЌЧѓГіЕуDЕФзјБъЃЛ
ЃЈ3ЃЉдкЕкЖўЮЪЕФЬѕМўЯТЃЌдкжБЯпDEЩЯДцдкЕуPЃЌЪЙЕУвдCЁЂDЁЂPЮЊЖЅЕуЕФШ§НЧаЮгыЁїDOCЯрЫЦЃЌЧыФужБНгаДГіЫљгаТњзуЬѕМўЕФЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
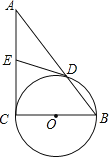
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌвдBCЮЊжБОЖЕФЁбOНЛABгкЕуDЃЌЁбOЕФЧаЯпDEНЛACгкЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEЪЧACжаЕуЃЛ
ЃЈ2ЃЉШєAB=10ЃЌBC=6ЃЌСЌНгCDЃЌOEЃЌНЛЕуЮЊFЃЌЧѓOFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ-6ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЕуCдкжБЯп![]() ЩЯЃЌдђЪЙЁїABCЪЧжБНЧШ§НЧаЮЕФЕуCЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
ЩЯЃЌдђЪЙЁїABCЪЧжБНЧШ§НЧаЮЕФЕуCЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
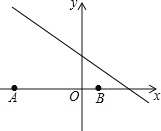
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com