
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
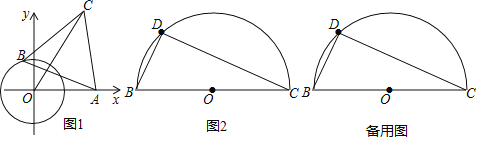
如图1,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值.
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)请直接写出线段OC的最大值.
(迁移拓展)
(3)如图2,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.
【答案】[解决问题](1)OC=AE,(2)OC的最大值为3.[迁移拓展](3)AC的最大值为2![]() +2
+2![]() .AC的最小值为2
.AC的最小值为2![]() ﹣2
﹣2![]() .
.
【解析】
(1)结论:OC=AE.只要证明△CBO≌△ABE即可;
(2)当E、O、A共线,AE有最大值,此时OC有最大值,据此求解即可;
(3)当点A在线段BD的左侧时,以BC为边作等边三角形△BCM,由△ABC≌△DBM,推出AC=MD,推出欲求AC的最大值,只要求出DM的最大值即可,当点D在BC上方,DM⊥BC时,DM的值最大;当点A在线段BD的左侧时,同理可求AC的最小值.
解:【解决问题】
(1)如图1中,结论:OC=AE,

理由:∵△ABC,△BOE都是等边三角形,
∴BC=BA,BO=BE,∠CBA=∠OBE=60°,
∴∠CBO=∠ABE,
∴△CBO≌△ABE(SAS),
∴OC=AE.
(2)在△AOE中,AE≤OE+OA,
∴当E、O、A共线,
∴AE的最大值为3,
∴OC的最大值为3.
【迁移拓展】
(3)如图2中,以BC为边作等边三角形△BCM,

∵∠ABD=∠CBM=60°,
∴∠ABC=∠DBM,且AB=DB,BC=BM,
∴△ABC≌△DBM(SAS),
∴AC=MD,
∴欲求AC的最大值,只要求出DM的最大值即可,
∵BC=4![]() =定值,∠BDC=90°,
=定值,∠BDC=90°,
∴点D在以BC为直径的⊙O上运动,
由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2![]() +2
+2 ![]() ,
,
∴AC的最大值为2![]() +2
+2 ![]() .
.
当点A在线段BD的右侧时,同理可得AC的最小值为2![]() -2
-2![]() .
.
综上所述AC的最大值为2![]() +2
+2 ![]() ,最小值为2
,最小值为2![]() -2
-2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
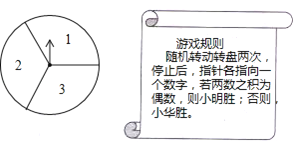
(1)现随机转动转盘一次,停止后,指针指向2的概率为 ;
(2)小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
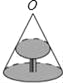
【题目】如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:当a>0且x>0时,因为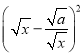 ≥0,所以
≥0,所以![]() ,从而
,从而![]() ≥
≥![]() (当x=
(当x=![]() 时取等号).
时取等号).
设函数![]() =
=![]() (
(![]() >0,x>0),由上述结论可知,当x=
>0,x>0),由上述结论可知,当x=![]() 时,该函数有最小值为
时,该函数有最小值为![]() .
.
应用举例:已知函数![]() =x(x>0)与函数
=x(x>0)与函数![]() =
=![]() (x>0),则当x=
(x>0),则当x=![]() =2时,
=2时,![]() =
=![]() 有最小值为
有最小值为![]() =4.
=4.
解决问题:
(1)已知函数![]() =
=![]() (x>-3)与函数
(x>-3)与函数![]() =
=![]() (x>-3),当x为何值时,
(x>-3),当x为何值时,![]() 有最小值?最小值是多少?
有最小值?最小值是多少?
(2)已知某设备租赁使用成本包含以下三部分:一是设备的安装调试费用,共490元;二是设备的租赁使用费用,每天200元;三是设备的折旧费用,它与使用天数的平方成正比,比例系数为0.001.若设该设备的租赁使用天数为x天,则当x取何值时,该设备平均每天的租赁使用成本最低?最低是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州区初中数学教研工作坊到重庆某中学开展研讨活动,先后乘坐甲、乙两辆汽车从万州出发前往相距250千米的重庆,乙车先出发匀速行驶,一段时间后,甲车出发匀速追赶,途中因油料不足,甲到服务区加油花了6分钟,为了尽快追上乙车,甲车提高速度仍保持匀速行驶,追上乙车后继续保持这一速度直到重庆,如图是甲、乙两车之间的距离s(km),乙车出发时间t(h)之间的函数关系图象,则甲车从万州出发到重庆共花费了_____小时.

查看答案和解析>>
科目:初中数学 来源: 题型:
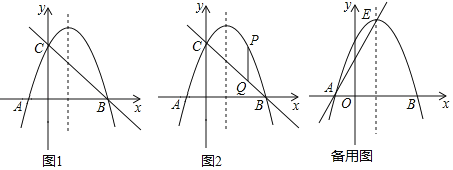
【题目】如图1,抛物线y=﹣x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,连接BC.
(1)求直线BC的解析式;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ∥y轴交BC于Q,当线段PQ的长度最大时,在x轴上找一点M,使PM+CM的值最小,求PM+CM的最小值;
(3)抛物线的顶点为点E,连接AE,在抛物线上是否存在一点N,使得直线AN与直线AE的夹角为45度,若存在请直接写出满足条件的点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线过A(1,0)、B(﹣3,0),C(0,﹣3)三点,直线AD交抛物线于点D,点D的横坐标为﹣2,点P(m,n)是线段AD上的动点,过点P的直线垂直于x轴,交抛物线于点Q.
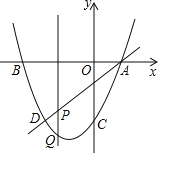
(1)求直线AD及抛物线的解析式;
(2)求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平面内是否存在整点(横、纵坐标都为整数)R,使得P、Q、D、R为顶点的四边形是平行四边形?若存在,求出点R的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com