
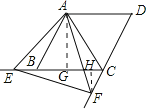
【题目】如图,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 的延长线上,点
的延长线上,点![]() 在
在![]() 的延长线上,有下列结论:①
的延长线上,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() .则其中正确结论的个数是( )
.则其中正确结论的个数是( )

A.1个B.2个C.3个D.4个
【答案】B
【解析】
①只要证明![]() 即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点
即可判断;②根据等边三角形的性质以及三角形外角的性质即可判断;③根据相似三角形的判定方法即可判断;④求得点![]() 到
到![]() 的距离即可判断.综上即可得答案.
的距离即可判断.综上即可得答案.
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∵∠ABC=60°,
∴![]() 是等边三角形,
是等边三角形,
∴∠ACD=∠ACB=60°,AB=AC,
∴∠ABE=∠ACF=120°,
∵![]() ,
,
∴∠BAE+∠BAF=∠CAF+∠BAF=60°,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() .故①正确;
.故①正确;
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故②正确;
,故②正确;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 和
和![]() 不会相似,故③不正确;
不会相似,故③不正确;
过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴点![]() 到
到![]() 的距离为
的距离为![]() ,故④不正确.
,故④不正确.
综上,正确结论有①②,共2个,
故选B.


科目:初中数学 来源: 题型:
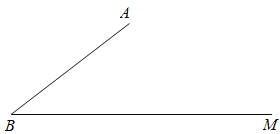
【题目】如图,已知∠ABM=30°,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是 ;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=![]() ;③△ABC的面积为126.
;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向终点
向终点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,它们的速度均为每秒5个单位长度,点
运动,它们的速度均为每秒5个单位长度,点![]() 到达终点时,
到达终点时,![]() 、
、![]() 同时停止运动.当点
同时停止运动.当点![]() 不与点
不与点![]() 、
、![]() 重合时,过点
重合时,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,以
,以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,运动时间为
,运动时间为![]() 秒.
秒.
(1)用含![]() 的代数式表示
的代数式表示![]() 的长为________;
的长为________;
(2)是否存在某一时刻![]() ,使四边形
,使四边形![]() 为矩形,若存在,求出
为矩形,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)![]() 时,求
时,求![]() 与
与![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
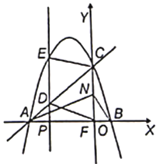
【题目】如图,抛物线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() 、
、![]() ,其中有
,其中有![]() ,
,![]() ,过抛物线对称轴左侧的一点
,过抛物线对称轴左侧的一点![]() 做
做![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 上运动,点
上运动,点![]() 是
是![]() 上的动点,
上的动点,![]() 连接
连接![]() ,
,![]() .
.
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)求![]() 的最小值;
的最小值;
(3)点![]() 是对称轴的左侧抛物线上的一个点,当
是对称轴的左侧抛物线上的一个点,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
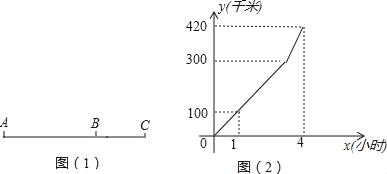
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.点D为BC中点,E为边AB上一动点(不与A、B点重合),以点D为直角顶点、以射线DE为一边作∠MDN=90°,另一条边DN与边AC交于点F.下列结论中正确结论是( )
①BE=AF;
②△DEF是等腰直角三角形;
③无论点E、F的位置如何,总有EF=DF+CF成立;
④四边形AEDF的面积随着点E、F的位置不同发生变化.
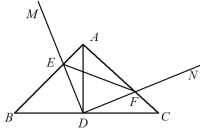
A.①③B.②③C.①②D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
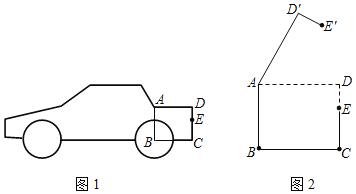
【题目】图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD′E′的位置(如图2所示).已知AD=96厘米,DE=28厘米,EC=42厘米.
(1)求点D′到BC的距离;
(2)求E、E′两点的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com