
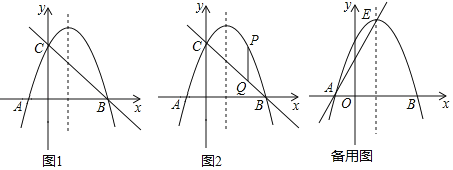
【题目】如图1,抛物线y=﹣x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,连接BC.
(1)求直线BC的解析式;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ∥y轴交BC于Q,当线段PQ的长度最大时,在x轴上找一点M,使PM+CM的值最小,求PM+CM的最小值;
(3)抛物线的顶点为点E,连接AE,在抛物线上是否存在一点N,使得直线AN与直线AE的夹角为45度,若存在请直接写出满足条件的点N的坐标,若不存在,请说明理由.
【答案】(1)y=﹣x+3;(2)![]() ;(3)点N的坐标为:(﹣
;(3)点N的坐标为:(﹣![]() ,
,![]() ).
).
【解析】
(1)抛物线x轴交于点A、B,与y轴交于点C,则点A、B、C的坐标分别为:(-1,0)、(3,0)、(0,3),即可求解;
(2)取点C关于x轴的对称点C′(0,-3),连接PC′交x轴于点M,则点M为所求点,此时PM+CM的最小,即可求解;
(3)设GM=AG=x,则GE=2x,AE=AG+EG=3x=![]() ,解得:x=
,解得:x=![]() ,HM2=AH2-OM2=(
,HM2=AH2-OM2=(![]() x)2
x)2![]() 4=
4=![]() ,故HM=
,故HM=![]() ,则点H(1,
,则点H(1,![]() ),将点A、H代入一次函数表达式并解得:直线AH(N)的表达式为:y=
),将点A、H代入一次函数表达式并解得:直线AH(N)的表达式为:y=![]() x+
x+![]() ,即可求解.
,即可求解.
解:(1)抛物线y=﹣x2+2x+3,抛物线x轴交于点A、B,与y轴交于点C,
则点A、B、C的坐标分别为:(﹣1,0)、(3,0)、(0,3),
∴将点B、C的坐标代入一次函数表达式:y=kx+b并解得:
直线BC的表达式为:y=﹣x+3;
(2)设点P(x,﹣x2+2x+3),则点Q(x,﹣x+3),
PQ=﹣x2+2x+3+x﹣3=﹣x2+3x,
当x=![]() 时,PQ有最大值,此时点P(
时,PQ有最大值,此时点P(![]() ,
,![]() );
);
取点C关于x轴的对称点C′(0,﹣3),连接PC′交x轴于点M,则点M为所求点,此时PM+CM的最小,
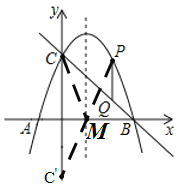
∴PM+CM的最小值=PC′=![]() ;
;
(3)如图,设直线AN交对称轴于点H,故点H作HG⊥AE于点G,对称轴交x轴于点M,
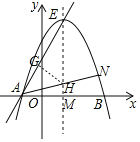
tan∠AEM=![]() ,设GM=AG=x,则GE=2x,
,设GM=AG=x,则GE=2x,
AE=AG+EG=3x=![]() ,解得:x=
,解得:x=![]() ,
,
HM2=AH2﹣OM2=(![]() )2﹣4=
)2﹣4=![]() ,
,
∴HM=![]() ,则点H(1,
,则点H(1,![]() ),
),
将点A、H代入一次函数表达式并解得:
直线AH(N)的表达式为:![]() ;
;
联立直线BC和直线AH,则:
 ,
,
解得:x=![]() 或﹣1(舍去﹣1),
或﹣1(舍去﹣1),
故点N的坐标为:(﹣![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
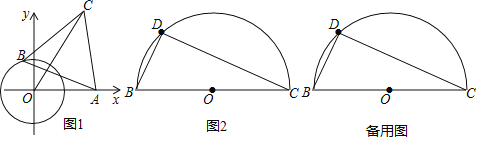
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
如图1,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值.
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)请直接写出线段OC的最大值.
(迁移拓展)
(3)如图2,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请求出AC的最值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州区中小学社会活动实践基地开展了人与社会、人与自然、人与自我的综合实践活动,其中高空项目能培养学生不怕困难,不畏艰险的精神.在高空项目中有以下四个特色实践活动:“A.合力制胜,B.空中断桥,C.绝壁飞胎,D.天罗地网”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题:
(1)本次一共调查了 名学生,并补全条形统计图;
(2)现有最喜爱A,B,C,D活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数y=-x2-2x+3说法正确的是( )
A. 当![]() 时,函数最大值4
时,函数最大值4
B. 当![]() 时,函数最大值2
时,函数最大值2
C. 将其图象向上平移3个单位后,图象经过原点
D. 将其图象向左平移3个单位后,图象经过原点
查看答案和解析>>
科目:初中数学 来源: 题型:
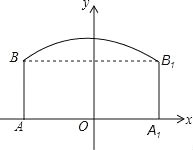
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长为16m,宽为6m,抛物线的最高点C离地面AA1的距离为8m.
(1)按如图所示的直角坐标系,求表示该抛物线的函数表达式.
(2)一大型汽车装载某大型设备后,高为7m,宽为4m,如果该隧道内设双向行车道,那么这辆贷车能否安全通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
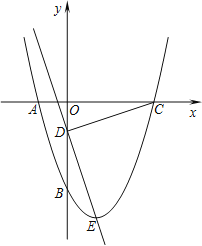
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com