练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】四川省公布了2018年经济数据GDP排行榜，成都市排名全省第一，GDP总量为15342亿元，数据“15342亿元”用科学记数法表示为（　　）

    A.1.5342×104亿元B.15.342×103亿元

    C.153.42×102亿元D.0.15342×105亿元

    【答案】A

    【解析】

    科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．

    解：15342亿＝1.5342×104亿．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：

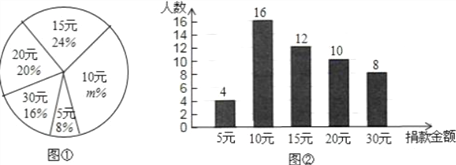
    （1）本次接受随机抽样调查的学生人数为 ，图①中m的值是 ；

    （2）求本次调查获取的样本数据的平均数、众数和中位数；

    （3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店5月1日举行促销优惠活动，当天到该商店购买商品有两种方案，方案一：用168元购买会员卡成为会员后，凭会员卡购买商店内任何商品，一律按商品价格的8折优惠；方案二：若不购买会员卡，则购买商店内任何商品一律按商品价格的9.5折优惠.

    （1）若小敏不购买会员卡，所购买商品的价格为120元时，实际应支付多少元？

    （2）请帮小敏算一算，她购买商品的价格为多少元时，两个方案所付金额相同？

    （3）购买商品的价格______元时，采用方案一更合算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC．

    （1）判断直线l与⊙O的位置关系，并说明理由；

    （2）若∠ABC的平分线BF交AD于点F，求证：BE=EF；

    （3）在（2）的条件下，若DE=4，DF=3，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（ ，0），B（0，2），则点B2016的坐标为 ．

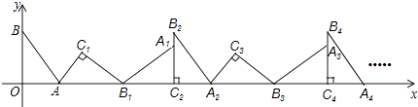
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某单位计划购买电脑若干台，经了解同一型号市场预售价均为每台5000元．现有两商场优惠促销，甲商场：购买不超过2台按原价销售，超过2台的部分每台打7折；乙商场：每台均打8折．

    （1）若学校购买5台，哪家商场较优惠？购买7台呢？

    （2）买多少台时两商场所需费用一样多？

    （3）你知道学校怎样选购更省钱？

    【答案】（1）购买5台，乙商场更优惠；购买7台，甲商场更优惠；（2）6；（3）答案见解析．

    【解析】试题分析：（1）根据甲乙两个商场的促销方案分别计算出学校购买5台和7台电脑所需的费用，比较即可；（2）设购买台时，两商场所需要费用一样多，根据费用一样多列出方程，解方程即可；（3）在（2）的基础上，比较即可.

    试题解析：

    （1）购买5台，甲商场：

    乙商场： ，， 乙商场更优惠．

    购买7台，甲商场：，乙商场： ．

    27500元＜28000元， 甲商场更优惠．

    （2）设购买台时，两商场所需要费用一样多，根据题意得

    ，解得： ．

    答：当购买台时，两商场所需要费用一样多．

    （3）当购买台数小于6时，在乙商场更省钱；

    当购买台数等于6时，两商场一样省钱；

    当购买台数大于6时，在甲商场更省钱．

    【题型】解答题
    【结束】
    26

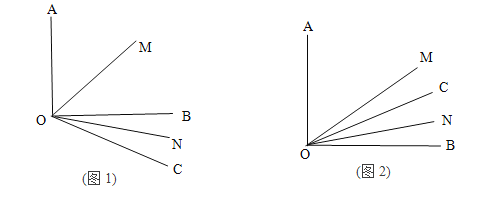
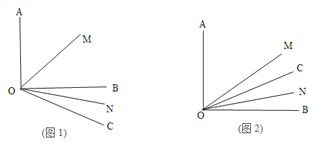
    【题目】已知∠AOB=90°，是锐角，ON平分，OM平分∠AOB．

    （1）如图1若=30°，求的度数？

    （2）若射线OC绕着点O运动到∠AOB的内部（如图2），在（1）的条件下求的度数；

    （3）若∠AOB=（90°≤＜180°），= （0°＜＜90°），请用含有的式子直接表示上述两种情况的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

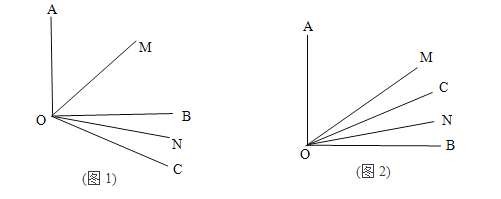
    【题目】已知∠AOB=90°，是锐角，ON平分，OM平分∠AOB．

    （1）如图1若=30°，求的度数？

    （2）若射线OC绕着点O运动到∠AOB的内部（如图2），在（1）的条件下求的度数；

    （3）若∠AOB=（90°≤＜180°），= （0°＜＜90°），请用含有的式子直接表示上述两种情况的度数．

    【答案】（1）60°；（2）30°；（3）①∠MON＝（＋），；②∠MON＝（－）．

    【解析】试题分析：（1）由于∠AOB=90°，∠BOC=30°，OM平分∠AOB，ON平分∠BOC，所以可以求得∠MOB和∠NOB的度数，进而求得∠MON的度数；（2）类比（1）的方法求解即可；（3）结合（1）（2）题的计算方法求解即可.

    试题解析：

    （1）∵OM平分∠AOB，ON平分∠BOC，

    ∴∠BOM＝∠AOB，∠BON＝∠BOC．

    ∵∠AOB＝90°，∠BOC＝30°，

    ∴∠BOM＝×90°＝45°，∠BON＝×30°＝15°，

    ∴∠MON＝∠BOM＋∠BON＝45°＋15°＝60°．

    （2）由（1）可知：∠BOM＝45°，∠BON＝15°，

    ∴∠MON＝∠BOM－∠BON＝45°－15°＝30°．

    （3）①∠MON＝（＋），②∠MON＝（－）．

    点睛：本题主要考查学生角平分线的定义及角的计算的理解和掌握，在解决角与角之间的关系时，要充分利用已知条件和图中的隐含条件.

    【题型】解答题
    【结束】
    27

    【题目】（1）已知线段AB=8cm，在线段AB上有一点C，且BC=4cm，M为线段AC的中点．

    ①求线段AM的长？

    ②若点C在线段AB的延长线上，AM的长度又是多少呢？

    （2）如图，AD=DB，E是BC的中点，BE=AC=2cm，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）阅读理解：实数， ，∵，∴，即。若（为定值），则，当且仅当时等式成立，即时， ，∴当时， 取得 值（填“最大”或“最小”）。

    （2）理解应用：函数，当x= 时， 。

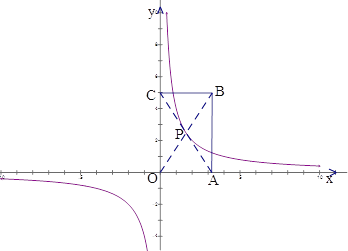
    （3）拓展应用：如图，双曲线经过矩形OABC的对角线交点P，求矩形OABC的最小周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（　　）

    A. x3+x3=x6B. x4÷x2=x2C. （m5）5=m10D. x2y3=（xy）3

    查看答案和解析>>

    同步练习册答案