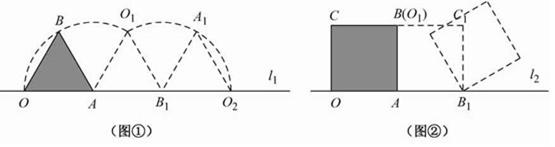
(本题满分9分)如图①,小慧同学把一个正三角形纸片(即△OAB)放在直线
l1上,OA边与直线
l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O
1处,点B运动到了点B
1处;小慧又将三角形纸片AO
1B
1绕点B
1按顺时针方向旋转120°,此时点A运动到了点A
1处,点O
1运动到了点O
2处(即顶点O经过上述两次旋转到达O
2处).
小慧还发现:三角形纸片在上述两次旋转的过程中,顶点O运动所形成的图形是两段
圆弧,即
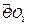
和
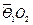
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
与直线
l1围成的图形面积等于扇形AOO
1的面积、△AO
1B
1的面积和扇形B
1O
1O
2的面积之
和.
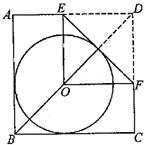
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线
l2上,OA
边与直线
l2重合,然后将正方形纸片绕着顶点^按顺时针方向旋转90°,此时点O运动到
了点O
1处(即点B处),点C运动到了点C
1处,点B运动到了点B
1处;小慧又将正方形
纸片AO
1C
1B
1绕顶点B
1按顺时针方向旋转90°,……,按上述方法经过若干次旋转后.她
提出了如下问题:
问题①:若正方形纸片OABC接上述方法经过3次旋转,求顶点O经过的路程,并
求顶点O在此运动过程中所形成的图形与直线
l2围成图形的面积;若正方形纸片OA BC
按上述方法经过5次旋转,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是
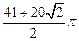
?
请你解答上述两个问题.



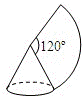

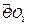 和
和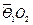 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧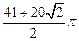 ?
?