
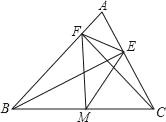
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
【答案】(1)11;(2)40°.
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半可得EM=MC=![]() BC,MF=MB=
BC,MF=MB= ![]() BC,然后根据三角形的周长的定义列式计算即可得解;
BC,然后根据三角形的周长的定义列式计算即可得解;
(2)根据等边对等角求出,∠ABC=∠MFB,∠ACB=∠MEC,再根据三角形的内角和定理求出∠BMF, ∠EMC,然后利用平角等于180°列式计算即可得解.
(1)∵CF⊥AB于F, M为BC的中点,∴ME=MC=![]() BC=
BC=![]() ×8=4,同理MF=MB=
×8=4,同理MF=MB= ![]() BC=
BC=![]() ×8=4,∴△EFM的周长=4+4+3=11;
×8=4,∴△EFM的周长=4+4+3=11;
(2)∵MF=MB,∴∠ABC=∠MFB=50°,同理∠ACB=∠MEC=60°,∴∠BMF=180°-50°-50°=80°,∠EMC=180°-60°-60°=60°,∴∠EMF=180°-80°-60°=40°.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
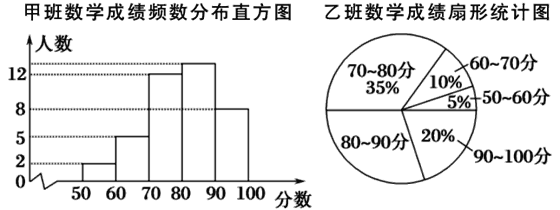
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⊙O是△ABC的外接圆,AB是直径,过 ![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP; 
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG; 
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ![]() ,求AC的长.
,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() 与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
与一次函数y=x+b的图形在第一象限相交于点A(1,﹣k+4).
(1)试确定这两函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△AOB的面积;
(3)根据图象直接写出反比例函数值大于一次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
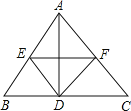
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
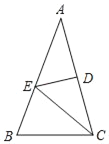
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块四边形田地ABCD,∠D=90°,AB=13m,BC=12m,CD=3m,DA=4m,则该四边形田地ABCD的面积为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com