
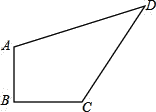
【题目】如图,一块草坪的形状为四边形ABCD,其中∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m,求这块草坪的面积。
【答案】这块草坪的面积为36平方厘米.
【解析】试题
如下图,连接AC,由已知条件根据勾股定理可得AC=5,结合CD=12,AD=13,由勾股定理逆定理可得∠ACD=90°,这样由四边形ABCD是由两个直角三角形构成的即可求出其面积了.
试题解析:
连接AC,
∵在Rt△ABC中,∠B=90°,AB=3,BC=4,
∴AC=5,
∵(AC)2+(CD)2=25+144=169,(AD)2=(13)2=169
∴(AC)2+(CD)2=(AD)2,
∴∠ACD=90°,即△ACD是直角三角形,
∴草坪面积=![]() S△ABC+
S△ABC+![]() S△ACD=
S△ACD=![]() ×3×4+
×3×4+![]() ×5×12=6+30=36.
×5×12=6+30=36.
即这块草坪的面积为36平方厘米.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
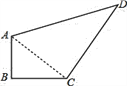
【题目】数学课上,柴老师出了一道题:如图,已知∠A=∠D,∠BCA=∠EFD.要使△ABC≌△DEF,你还应给出的条件是什么?下面四个同学做了回答:小马:“增加∠E=∠B;小李:“增加ED=BA;”小周:“增加AB=EF;”小胡:“增加AF=DC.”针对上面四个同学的回答,你认为正确的是_____.(填上你认为正确的同学的名字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新晚报举办的“万人户外徒步活动”中,为统计参加活动人员的年龄情况,从参加人员中随机抽取了若干人的年龄作为样本,进行数据统计,制成如图的条形统计图和扇形统计图(部分). 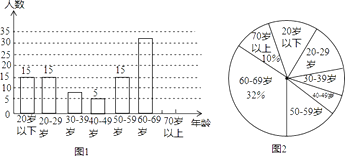
(1)本次活动统计的样本容量是多少?
(2)求本次活动中70岁以上的人数,并补全条形统计图;
(3)本次参加活动的总人数约为12000人,请你估算参加活动人数最多的年龄段的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
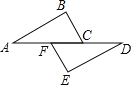
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
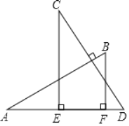
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
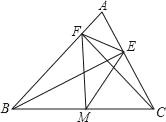
【题目】如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=3,BC=8,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( ) 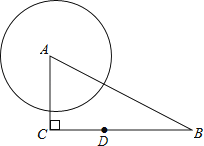
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
查看答案和解析>>
科目:初中数学 来源: 题型:
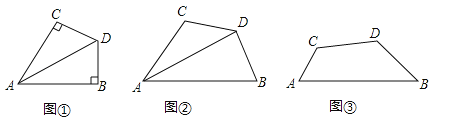
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( ) 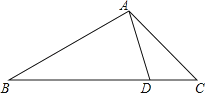
A.15
B.10
C.![]()
D.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com