
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
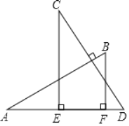
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
科目:初中数学 来源: 题型:
【题目】⊙O是△ABC的外接圆,AB是直径,过 ![]() 的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
的中点P作⊙O的直径PG,与弦BC相交于点D,连接AG、CP、PB.
(1)如图1,求证:AG=CP; 
(2)如图2,过点P作AB的垂线,垂足为点H,连接DH,求证:DH∥AG; 
(3)如图3,连接PA,延长HD分别与PA、PC相交于点K、F,已知FK=2,△ODH的面积为2 ![]() ,求AC的长.
,求AC的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人沿一条直路行走,此人离出发地的距离![]() 千米
千米![]() 与行走时间
与行走时间![]() 分钟
分钟![]() 的函数关系如图所示,请根据图象提供的信息回答下列问题:
的函数关系如图所示,请根据图象提供的信息回答下列问题:
![]() 此人离开出发地最远距离是______ 千米;
此人离开出发地最远距离是______ 千米;
![]() 此人在这次行走过程中,停留所用的时间为______ 分钟;
此人在这次行走过程中,停留所用的时间为______ 分钟;
![]() 由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米;
由图中线段OA可知,此人在这段时间内行走的速度是每小时______ 千米;
![]() 此人在120分钟内共走了______ 千米.
此人在120分钟内共走了______ 千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.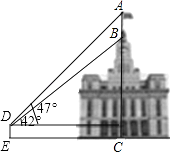
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( ) 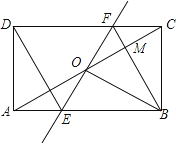
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.试猜想线段AD与AG的数量及位置关系,并证明你的猜想.
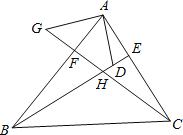
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com