
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( ) 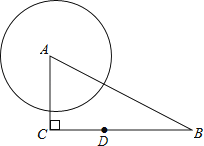
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
【答案】B
【解析】解:连接AD,
∵AC=4,CD=3,∠C=90°,
∴AD=5,
∵⊙A的半径长为3,⊙D与⊙A相交,
∴r>5﹣3=2,
∵BC=7,
∴BD=4,
∵点B在⊙D外,
∴r<4,
∴⊙D的半径长r的取值范围是2<r<4,
故选B.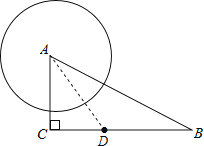
【考点精析】解答此题的关键在于理解点和圆的三种位置关系的相关知识,掌握圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r,以及对圆与圆的位置关系的理解,了解两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:
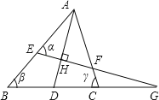
【题目】如图,AD平分∠BAC,EG⊥AD于H,则下列等式中成立的是 ( )
A. ∠α=![]() (∠β﹣∠γ) B. ∠α=
(∠β﹣∠γ) B. ∠α=![]() (∠β+∠γ) C. ∠G=
(∠β+∠γ) C. ∠G=![]() (∠β+∠γ) D. ∠G=
(∠β+∠γ) D. ∠G=![]() ∠α
∠α
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物BC顶部有一旗杆AB,且点A,B,C在同一条直线上,小红在D处观测旗杆顶部A的仰角为47°,观测旗杆底部B的仰角为42°已知点D到地面的距离DE为1.56m,EC=21m,求旗杆AB的高度和建筑物BC的高度(结果保留小数后一位).参考数据:tan47°≈1.07,tan42°≈0.90.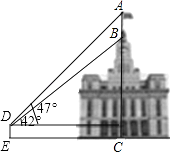
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AD⊥BC于D,DE∥AC于E,DF∥AB交AC于F,连接EF。
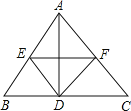
(1)当△ABC满足什么条件时,四边形AEDF是矩形;
(2)当△ABC满足什么条件时,四边形AEDF是正方形,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( ) 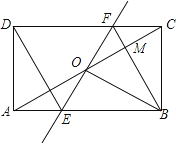
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上,某个一次函数的图形通过(5,0)、(10,﹣10)两点,判断此函数的图形会通过下列哪一点?( )
A.( ![]() ,9
,9 ![]() )
)
B.( ![]() ,9
,9 ![]() )
)
C.( ![]() ,9
,9 ![]() )
)
D.( ![]() ,9
,9 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
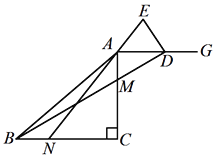
【题目】已知△ ABC 是等腰三角形,CA=CB,0°<∠ACB≤90°,点 M 在边 AC 上,点 N在边 BC 上(点 M、点 N 不与所在线段端点重合),BN=AM,连接 AN,BM.射线 AG∥BC,延长 BM 交射线 AG 于点 D,点 E 在直线 AN 上,且 AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△ BCM≌△ACN;
②求∠BDE 的度数;
(2)当∠ACB=ɑ ,其它条件不变时,∠BDE 的度数是 (用含ɑ 的代数式表示).
(3)若△ ABC 是等边三角形,AB=3![]() ,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com