
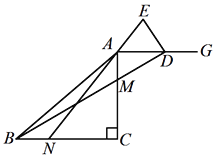
【题目】已知△ ABC 是等腰三角形,CA=CB,0°<∠ACB≤90°,点 M 在边 AC 上,点 N在边 BC 上(点 M、点 N 不与所在线段端点重合),BN=AM,连接 AN,BM.射线 AG∥BC,延长 BM 交射线 AG 于点 D,点 E 在直线 AN 上,且 AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△ BCM≌△ACN;
②求∠BDE 的度数;
(2)当∠ACB=ɑ ,其它条件不变时,∠BDE 的度数是 (用含ɑ 的代数式表示).
(3)若△ ABC 是等边三角形,AB=3![]() ,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
【答案】(1)详见解析;90°;(2)α或180-α;(3)![]() 或
或![]() .
.
【解析】
(1)①根据SAS证明即可;
②想办法证明∠ADE+∠ADB=90°即可;
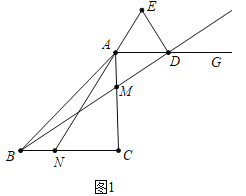
(2)分两种情形讨论求解即可,①如图2中,当点E在AN的延长线上时,②如图3中,当点E在NA的延长线上时;
(3)分两种情形求解即可,①如图4中,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K.解直角三角形即可.②如图5中,当CN=
时,作AK⊥BC于K.解直角三角形即可.②如图5中,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H.
时,作AK⊥BC于K,DH⊥BC于H.
(1)①如图1.
∵CA=CB,BN=AM,∴CB﹣BN=CA﹣AM,即CN=CM.
∵∠ACN=∠BCM,∴△BCM≌△ACN.
②如图1.
∵△BCM≌△ACN,∴∠MBC=∠NAC.
∵EA=ED,∴∠EAD=∠EDA.
∵AG∥BC,∴∠GAC=∠ACB=90°,∠ADB=∠DBC,∴∠ADB=∠NAC,∴∠ADB+∠EDA=∠NAC+∠EAD=∠ADB+∠EDA=180°﹣90°=90°,∴∠BDE=90°.
(2)如图2,当点E在AN的延长线上时.
易证:∠CBM=∠ADB=∠CAN,∠ACB=∠CAD.
∵EA=ED,∴∠EAD=∠EDA,∴∠CAN+∠CAD=∠BDE+∠ADB,∴∠BDE=∠ACB=α.
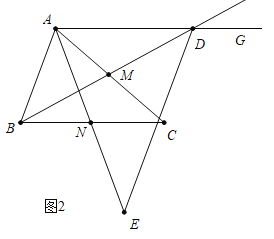
如图3,当点E在NA的延长线上时.
易证:∠1+∠2=∠CAN+∠DAC.
∵∠2=∠ADM=∠CBD=∠CAN,∴∠1=∠CAD=∠ACB=α,∴∠BDE=180°﹣α.
综上所述:∠BDE=α或180°﹣α.
故答案为:α或180°﹣α.
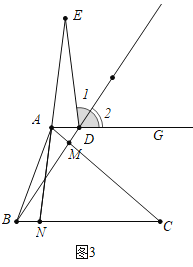
(3)如图4,当BN=![]() BC=
BC=![]() 时,作AK⊥BC于K,连结CD.
时,作AK⊥BC于K,连结CD.
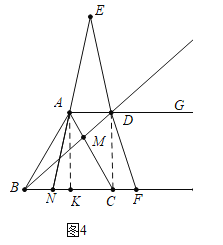
∵AD∥BC,∴![]() =
=![]() =
=![]() ,∴AD=
,∴AD=![]() ,AC=3
,AC=3![]() ,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,∴CF=NK=BK﹣BN=
,易证△ADC是直角三角形,则四边形ADCK是矩形,△AKN≌△DCF,∴CF=NK=BK﹣BN=![]() ﹣
﹣![]() =
=![]() .
.
如图5,当CN=![]() BC=
BC=![]() 时,作AK⊥BC于K,DH⊥BC于H.
时,作AK⊥BC于K,DH⊥BC于H.
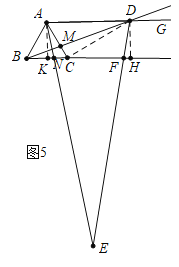
∵AD∥BC,∴![]() =
=![]() =2,∴AD=6
=2,∴AD=6![]() ,易证△ACD是直角三角形,由△ACK∽△CDH,可得CH=
,易证△ACD是直角三角形,由△ACK∽△CDH,可得CH=![]() AK=
AK=![]() ,由△AKN≌△DHF,可得KN=FH=
,由△AKN≌△DHF,可得KN=FH=![]() ,∴CF=CH﹣FH=4
,∴CF=CH﹣FH=4![]() .
.
综上所述:CF的长为![]() 或4
或4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( ) 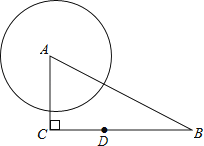
A.1<r<4
B.2<r<4
C.1<r<8
D.2<r<8
查看答案和解析>>
科目:初中数学 来源: 题型:
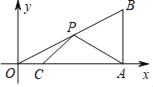
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( ) 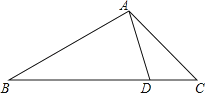
A.15
B.10
C.![]()
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC:S△ABC=1:3.其中正确的是__________________.(填所有正确说法的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:
第一个数是 ![]() ;
;
第二个数是 ![]() ;
;
第三个数是 ![]() ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于 ![]() .
.
(1)经过探究,我们发现: ![]()
设这列数的第5个数为a,那么 ![]() ,
, ![]() ,
, ![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于 ![]() ”;
”;
(3)设M表示 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,这2016个数的和,即
,这2016个数的和,即 ![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABC的边BC在x轴上,A,C两点的坐标分别为A(0,m),C(n,0),B(﹣5,0),且(n﹣3)2+![]() =0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
=0.一动点P从点B出发,以每秒2单位长度的速度沿射线BO匀速运动,设点P运动的时间为ts.
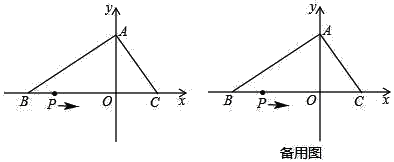
(1)求A,C两点的坐标;
(2)连接PA,若△PAB为等腰三角形,求点P的坐标;
(3)当点P在线段BO上运动时,在y轴上是否存在点Q,使△POQ与△AOC全等?若存在,请求出t的值并直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com