
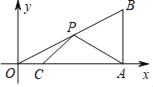
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( ) 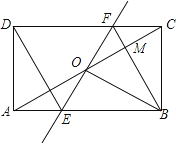
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上,某个一次函数的图形通过(5,0)、(10,﹣10)两点,判断此函数的图形会通过下列哪一点?( )
A.( ![]() ,9
,9 ![]() )
)
B.( ![]() ,9
,9 ![]() )
)
C.( ![]() ,9
,9 ![]() )
)
D.( ![]() ,9
,9 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a1+a2+…+a30+a31与b1+b2+…+b30+b31均为等差级数,且皆有31项.若a2+b30=29,a30+b2=﹣9,则此两等差级数的和相加的结果为多少?( )
A.300
B.310
C.600
D.620
查看答案和解析>>
科目:初中数学 来源: 题型:
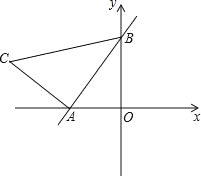
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
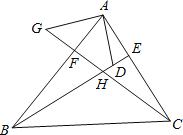
【题目】如图,在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.试猜想线段AD与AG的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
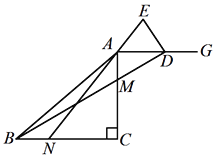
【题目】已知△ ABC 是等腰三角形,CA=CB,0°<∠ACB≤90°,点 M 在边 AC 上,点 N在边 BC 上(点 M、点 N 不与所在线段端点重合),BN=AM,连接 AN,BM.射线 AG∥BC,延长 BM 交射线 AG 于点 D,点 E 在直线 AN 上,且 AE=DE.
(1)如图,当∠ACB=90°时,
①求证:△ BCM≌△ACN;
②求∠BDE 的度数;
(2)当∠ACB=ɑ ,其它条件不变时,∠BDE 的度数是 (用含ɑ 的代数式表示).
(3)若△ ABC 是等边三角形,AB=3![]() ,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
,点 N 是 BC 边上的三等分点,直线 ED 与直线 BC 交于点 F,请直接写出线段 CF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体健康无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A,B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加添加剂2克,B饮料每瓶需加添加剂3克,饮料加工厂生产了A,B两种饮料各多少瓶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com