
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
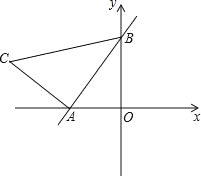
【答案】(1)A(﹣1,0),k=2;(2)C(﹣3,1);(3)P坐标为(2,1).
【解析】
(1)对于直线y=kx+2,令x=0求出y的值,确定出B坐标,得到OB的长,根据OA与OB比值求出OA的长,确定出A坐标,代入直线方程即可求出k的值;
(2)过C作CM垂直于x轴,利用同角的余角相等得到一对角相等,再由一对直角相等,以及AC=AB,利用AAS得到三角形ACM与三角形BAO全等,由全等三角形对应边相等得到CM=OA,AM=OB,由AM+OA求出OM的长,即可确定出C坐标;
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y= ![]() x第一象限上取一点P,连接BP,AP,设点P(m,
x第一象限上取一点P,连接BP,AP,设点P(m,![]() m),由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积,求出三角形AOB面积,两者相等求出m的值,即可确定出P坐标.
m),由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积,求出三角形AOB面积,两者相等求出m的值,即可确定出P坐标.
(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
∵OA:OB=![]() ,∴OA=1,即A(﹣1,0),
,∴OA=1,即A(﹣1,0),
将x=﹣1,y=0代入直线解析式得:0=﹣k+2,即k=2;
(2)过C作CM⊥x轴,可得∠AMC=∠BOA=90°,
∴∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,
∴∠ACM=∠BAO,
在△CAM和△ABO中,
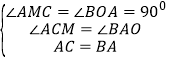 ,
,
∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=1,即OM=OA+AM=1+2=3,
∴C(﹣3,1);
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=![]() x第一象限上取一点P,连接BP,AP,
x第一象限上取一点P,连接BP,AP,
设点P(m,![]() m),
m),
∴S△ABP=S△ABO+S△BPO﹣S△AOP=1+m﹣![]() m=1+
m=1+![]() m,而S△ABC=
m,而S△ABC=![]() ABAC=
ABAC=![]() AB2=
AB2=![]() (12+22)=
(12+22)=![]() ,
,
可得1+![]() m=
m=![]() ,
,
解得:m=2,
则P坐标为(2,1).


科目:初中数学 来源: 题型:
【题目】有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
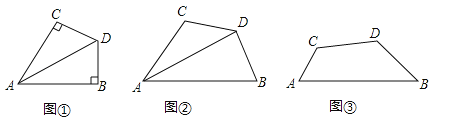
【题目】感知:如图1,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图3,四边形ABCD中,∠B=45°,∠C=135°,DB=DC=a,则AB﹣AC= (用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为10,圆O分别与AB、AD相切于E、F两点,且与BG相切于G点.若AO=5,且圆O的半径为3,则BG的长度为何?( ) 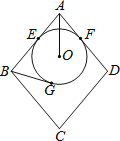
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
),点C的坐标为(1,0),且∠B=60°,点P为斜边OB上的一个动点,则PA+PC的最小值为_____.
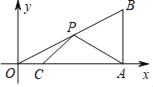
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
⑴.在图中作出△ABC关于y轴对称的△A1B1C1.
⑵.写出点A1,B1,C1的坐标(直接写出答案).
A1 B1 C1 ;
⑶.△A1B1C1的面积为 .
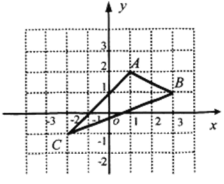
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( ) 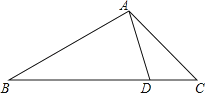
A.15
B.10
C.![]()
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列按一定顺序和规律排列的数:
第一个数是 ![]() ;
;
第二个数是 ![]() ;
;
第三个数是 ![]() ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于 ![]() .
.
(1)经过探究,我们发现: ![]()
设这列数的第5个数为a,那么 ![]() ,
, ![]() ,
, ![]() ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于 ![]() ”;
”;
(3)设M表示 ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,这2016个数的和,即
,这2016个数的和,即 ![]() ,
,
求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D,F分别在AC,BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( ) 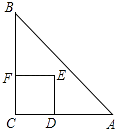
A.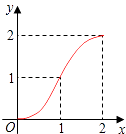
B.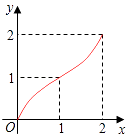
C.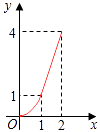
D.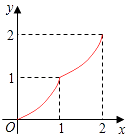
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com