
 如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.
如图,大半圆的弦AB平行于直径CD,且与小半圆相切,已知AB=16cm,求图中阴影部分的面积.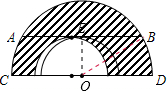 解:连接OB,作OE⊥AB于E,
解:连接OB,作OE⊥AB于E,| 1 |
| 2 |
| OB2 |
| 2 |
| OE2 |
| 2 |
| EB2 |
| 2 |


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、亏28元 | B、赚28元 |
| C、赚14元 | D、亏14元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 质量档次 | 1 | 2 | … | x | … | 10 |
| 日产量(件) | 95 | 90 | … | 100-5x | … | 50 |
| 单件利润(万元) | 6 | 8 | … | 2x+4 | … | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:
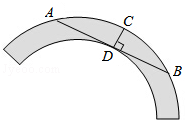 如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,作CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com