
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
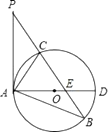
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长.
【答案】(1)证明见解析(2)2![]()
【解析】试题分析:(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案;
(2)首先得出△CAG∽△BAC,进而得出AC2=AG·AB,求出AC即可.
试题解析:(1)连接CD,如图,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD+∠D=90°,
∵∠PAC=∠PBA,∠D=∠PBA,
∴∠CAD+∠PAC=90°,
即∠PAD=90°,
∴PA⊥AD,
∴PA是⊙O的切线;
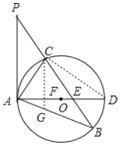
(2)∵CF⊥AD,
∴∠ACF+∠CAF=90°,∠CAD+∠D=90°,
∴∠ACF=∠D,
∴∠ACF=∠B,
而∠CAG=∠BAC,
∴△ACG∽△ABC,
∴AC:AB=AG:AC,
∴AC2=AGAB=12,
∴AC=2![]() .
.


科目:初中数学 来源: 题型:
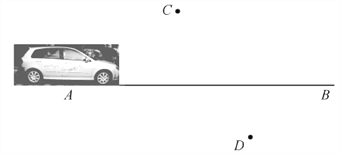
【题目】如图所示,一辆汽车在直线形的公路AB上由A向B行驶,C,D分别是位于公路AB两侧的村庄.
(1)该汽车行驶到公路AB上的某一位置C′时距离村庄C最近,行驶到D′位置时,距离村庄D最近,请在公路AB上作出C′,D′的位置(保留作图痕迹);
(2)当汽车从A出发向B行驶时,在哪一段路上距离村庄C越来越远,而离村庄D越来越近?(只叙述结论,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+bx+a=0有一个根是﹣a(a≠0),则a﹣b的值为( )
A.a﹣b=1B.a﹣b=﹣1C.a﹣b=0D.a﹣b=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com