
【题目】如果2x3my4与﹣3x9y2n是同类项,那么m+n值为_____.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】为迎接“劳动周”的到来,某校将九(1)班50名学生本周的课后劳动时间比上周都延长了10分钟,则该班学生本周劳动时间的下列数据与上周比较不发生变化的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= ![]() BD;
BD;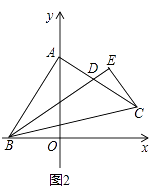
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.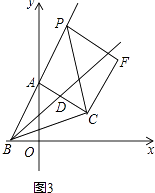
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
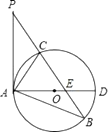
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2-8x+3=0,此方程可化为( )
A. (x-4)2=13 B. (x+4)2=13 C. (x-4)2=19 D. (x+4)2=19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现用甲、乙两种运输车将46t抗旱物资运往灾区,甲种运输车载重5t,乙种运输车载重4t,安排车辆不超过10辆,则甲种运输车至少应安排( )
A.4辆
B.5辆
C.6辆
D.7辆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com