
【题目】在△ABC中,∠BAC=90°,AB=AC.
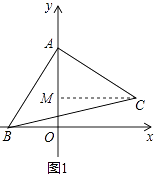
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
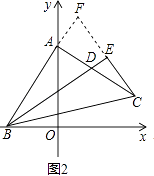
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= ![]() BD;
BD;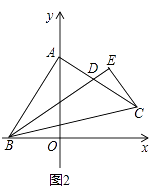
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.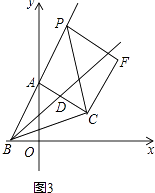
【答案】
(1)
解:如图1中,作CM⊥OA垂足为M,
∵∠AOB=∠BAC=90°,
∴∠BAO+∠CAM=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠CAM,
在△ABO和△CAM中,
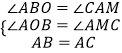 ,
,
∴△ABO≌△CAM,
∴MC=AO=4,AM=BO=2,MO=AO﹣AM=2,
∴点C坐标(4,2)
(2)
证明:如图2,延长CE,BA相交于点F,
∵∠EBF+∠F=90°,∠ACF+∠F=90°,
∴∠EBF=∠ACF,
在△ABD和△ACF中 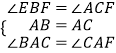 ,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
在△BCE和△BFE中, 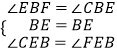 ,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∴CE= ![]() BD
BD
(3)
解:结论:点Q恒在射线BD上,
理由如下:
如图3中作QE⊥PF,QG⊥FC,QH⊥PC,QM⊥BP,QN⊥BC,垂足分别为E、G、H、M、N.
在四边形QMBN中,∵∠QMB=∠QNB=90°,
∴∠MQN=180°﹣∠ABC=135°,
同理可证:∠HQG=135°,
∴∠MQN=∠HQG,
∴∠MQH=∠GQN,
∵PQ平分∠FPC,QF平分∠PFC,QE⊥PF,QH⊥PC,QG⊥FC,
∴QE=QH=QG,∠QPH= ![]() ∠CPF=22.5°,
∠CPF=22.5°,
∵∠PMQ=∠PHQ=90°,
∴M、H、Q、P四点共圆,
∴∠HMP=∠HPQ=22.5°,同理∠QNG=22.5°,
∴∠FMQ=∠QNG,
在△MHQ和△NGQ中,
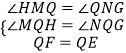 ,
,
∴△MHQ≌△NGQ,
∴QM=QN,
∵QM⊥BP,QN⊥BC,
∴BQ平分∠ABC,
∴点Q恒在射线BD上
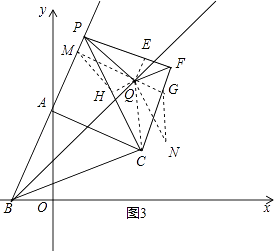
【解析】(1)要求点C坐标,作CM⊥AO,只要利用全等三角形的性质求出OM、CM即可;(2)延长CE、BA相交于点F.可以证明Rt△ABD≌Rt△ACF,再证明△BCE≌△BFE得到CE=EF,就可以得出结论;(3)点Q是否恒在射线BD上,只要证明QM=QN,只要证明△M,HQ≌△NGQ即可.
【考点精析】根据题目的已知条件,利用全等三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等.


科目:初中数学 来源: 题型:
【题目】粤海铁路是我国第一条横跨海峡的铁路通道,设计年输送货物能力为11 000 000吨,用科学记数法应记为( )
A.11×106吨
B.1.1×107吨
C.11×107吨
D.1.1×108吨
查看答案和解析>>
科目:初中数学 来源: 题型:
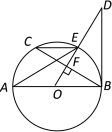
【题目】如图,AB是⊙O直径,OD⊥弦BC与点F,且交⊙O于点E,且∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC=![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
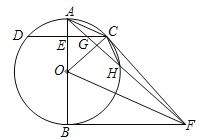
【题目】如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连接AF,CF,AF与CD交于点G,与⊙O交于点H,连接CH.
(1)求证:CF是⊙O的切线;
(2)求证:EG=GC;
(3)若cos∠AOC=![]() ,⊙O的半径为9,求CH的长.
,⊙O的半径为9,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
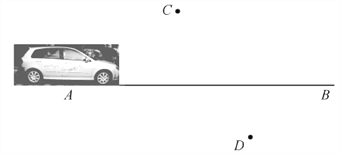
【题目】如图所示,一辆汽车在直线形的公路AB上由A向B行驶,C,D分别是位于公路AB两侧的村庄.
(1)该汽车行驶到公路AB上的某一位置C′时距离村庄C最近,行驶到D′位置时,距离村庄D最近,请在公路AB上作出C′,D′的位置(保留作图痕迹);
(2)当汽车从A出发向B行驶时,在哪一段路上距离村庄C越来越远,而离村庄D越来越近?(只叙述结论,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. 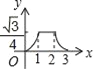 B.
B.  C.
C. 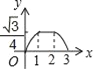 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+bx+a=0有一个根是﹣a(a≠0),则a﹣b的值为( )
A.a﹣b=1B.a﹣b=﹣1C.a﹣b=0D.a﹣b=±1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com