
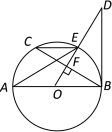
【题目】如图,AB是⊙O直径,OD⊥弦BC与点F,且交⊙O于点E,且∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC=![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
【答案】(1)直线BD和⊙O相切,证明见解析;(2)![]()
【解析】(1)因为同弧所对的圆周角相等,所以有∠AEC=∠ABC,又∠AEC=∠ODB,所以∠ABC=∠ODB,OD⊥弦BC,即∠ABC+∠BOD=90°,则有∠ODB+∠BOD=90°,即BD垂直于AB,所以BD为切线.
(2)由垂径定理可得FB=FC=4,再由三角关系得到DF=![]() ,BD可由勾股定理求出,再由△DBF∽△ODB,并根据对应线段成比例求出OD.
,BD可由勾股定理求出,再由△DBF∽△ODB,并根据对应线段成比例求出OD.
解:(1)直线BD和⊙O相切
证明:∵∠AEC=∠ODB,∠AEC=∠ABC
∴∠ABC=∠ODB
∵OD⊥BC
∴∠DBC+∠ODB=90°
∴∠DBC+∠ABC=90°
∴∠DBO=90°
∴直线BD和⊙O相切.
(2)∵OD⊥BC
∴FB=FC=4
∵tan∠AEC=tan∠ODB=3:4
∴BF:DF =3:4 ,
∴DF=![]()
利用勾股定理可求得BD=![]()
通过证明△DBF∽△ODB,利用相似比可得OD:DB=BD:FD
所以求出OD=![]()


科目:初中数学 来源: 题型:
【题目】为迎接“劳动周”的到来,某校将九(1)班50名学生本周的课后劳动时间比上周都延长了10分钟,则该班学生本周劳动时间的下列数据与上周比较不发生变化的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,P(a,b)是△ABC的边AC上一点:
,P(a,b)是△ABC的边AC上一点:
(1)将![]() 绕原点
绕原点![]() 逆时针旋转90°得到
逆时针旋转90°得到![]() ,请在网格中画出
,请在网格中画出![]() ,旋转过程中点A所走的路径长为 .
,旋转过程中点A所走的路径长为 .
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2,并写出点A2、的坐标:A2( ).
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
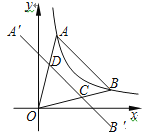
【题目】如图,点A,B在反比例函数y=![]() (x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为
(x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为![]() ,则点A的坐标为_______.
,则点A的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= ![]() BD;
BD;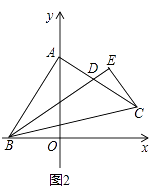
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.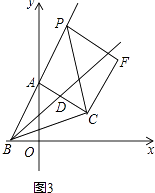
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现用甲、乙两种运输车将46t抗旱物资运往灾区,甲种运输车载重5t,乙种运输车载重4t,安排车辆不超过10辆,则甲种运输车至少应安排( )
A.4辆
B.5辆
C.6辆
D.7辆
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com