
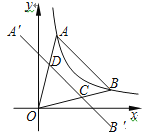
【题目】如图,点A,B在反比例函数y=![]() (x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为
(x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为![]() ,则点A的坐标为_______.
,则点A的坐标为_______.
【答案】(![]() ,2)
,2)
【解析】∵反比例函数y= ![]() ,关于直线y=x对称, OA=OB,
,关于直线y=x对称, OA=OB,
∴A、B关于直线y=x对称,
设点A的坐标为(m, ![]() ),则点B的坐标为(
),则点B的坐标为( ![]() ,m),则点A′的坐标为(-m,
,m),则点A′的坐标为(-m, ![]() ),点B′的坐标为(
),点B′的坐标为(![]() ,-m),
,-m),
∴直线OB的解析式为y=m2x, 直线A′B′的解析式为y=-x+![]() -m,
-m,
由 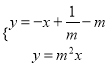 ,解得
,解得 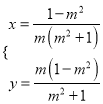
∴C[ 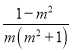 ,
, ![]() ],根据对称性可知D[
],根据对称性可知D[ ![]() ,
, 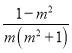 ],
],
如图,设A′B′交x轴于F,交y轴于E,连接AA′,作DN⊥OF于N,CM⊥OE于M,DN交CM于G.
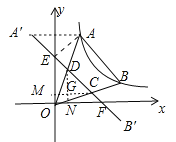
∵OE=OF= ![]() -m,
-m,
∴∠OEF=∠OFE=45°,
∴∠A′EA=90°,AE=![]() m,
m,
在Rt△CDG中,∵DG=CG,CD= ![]() CG=
CG= ![]() [
[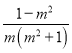 -
-![]() ].
].
同理可得,AB= ![]() (
(![]() -m),
-m),
∵四边形![]() ,
,
∴ 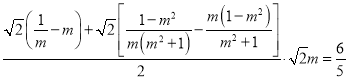
整理得![]() ,解得
,解得![]() ,∵m>0,
,∵m>0,
∴m=![]() ,
,
∴A( ![]() ,2).
,2).


科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O. 
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
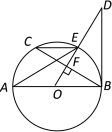
【题目】如图,AB是⊙O直径,OD⊥弦BC与点F,且交⊙O于点E,且∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC=![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
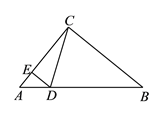
【题目】如图,在△ABC中(BC>AC),∠ACB=90°,点D在AB边上,DE⊥AC于点E.设点F在线段EC上,点G在射线CB上,以F,C,G为顶点的三角形与△EDC有一个锐角相等,FG交CD于点P,问:线段CP可能是△CFG的高线还是中线?或两者都有可能?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
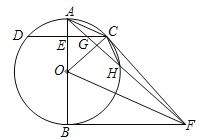
【题目】如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连接AF,CF,AF与CD交于点G,与⊙O交于点H,连接CH.
(1)求证:CF是⊙O的切线;
(2)求证:EG=GC;
(3)若cos∠AOC=![]() ,⊙O的半径为9,求CH的长.
,⊙O的半径为9,求CH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. 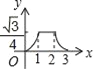 B.
B.  C.
C. 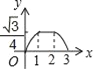 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com