
【题目】如图,已知AB是⊙O的直径,C是⊙O上任一点(不与A,B重合),AB⊥CD于E,BF为⊙O的切线,OF∥AC,连接AF,CF,AF与CD交于点G,与⊙O交于点H,连接CH.
(1)求证:CF是⊙O的切线;
(2)求证:EG=GC;
(3)若cos∠AOC=![]() ,⊙O的半径为9,求CH的长.
,⊙O的半径为9,求CH的长.
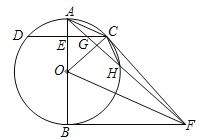
【答案】(1)证明见解析;
(2)证明见解析;
(3)CH的长为![]()
【解析】试题分析:(1)根据OF∥AC,OA=OC,判断出∠BOF=∠COF;然后根据全等三角形判定的方法,判断出△BOF≌△COF,推得∠OCF=∠OBF=90°,再根据点C在⊙O上,即可判断出FC是⊙O的切线. (2)根据已知条件△AEC∽△OBF,根据相似三角形的性质可得![]() =
= ![]() ,再由∠EAG=∠BAF,∠AEG=∠ABF,可得△AEG∽△ABF,即可得
,再由∠EAG=∠BAF,∠AEG=∠ABF,可得△AEG∽△ABF,即可得![]() =
= ![]() ,因AB=2OB,所以
,因AB=2OB,所以![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,所以EC=2EG,即可得结论EG=GC ;
,所以EC=2EG,即可得结论EG=GC ;
(3)延长CO交⊙O于K,连接HK,易证∠CAF=∠HCF,再由∠AFC=∠CFH,即可判断△ACF∽△CHF,根据相似三角形的性质可得![]() =
= ![]() ,因cos∠AOC=
,因cos∠AOC= ![]() ,OC=9,可得
,OC=9,可得![]() =
= ![]() =
= ![]() ,即可求得OE=6,所以AE=3,EC 2=OC 2-OE 2=45,由勾股定理可得AC=
,即可求得OE=6,所以AE=3,EC 2=OC 2-OE 2=45,由勾股定理可得AC= ![]() =3
=3![]() ,再由
,再由![]() =
= ![]() ,可求得BF=9
,可求得BF=9![]() ,再由勾股定理可得AF=
,再由勾股定理可得AF= ![]() =27,BF、CF都是⊙O的切线,根据切线长定理可得CF=BF=9
=27,BF、CF都是⊙O的切线,根据切线长定理可得CF=BF=9![]() ,由此求得CH=
,由此求得CH=![]() .
.
试题解析:
(1)∵BF为⊙O的切线,∴∠OBF=90°
∵OA=OC,∴∠OAC=∠OCA
∵OF∥AC,∴∠OAC=∠BOF,∠OCA=∠COF
∴∠BOF=∠COF
又OB=OC,OF=OF,∴△OBF≌△OCF
∴∠OCF=∠OBF=90°
∴CF是⊙O的切线
(2)∵AB⊥CD,∴∠AEC=90°
∴∠AEC=∠OBF
又∠EAC=∠BOF,∴△AEC∽△OBF
∴![]() =
= ![]()
∵∠EAG=∠BAF,∠AEG=∠ABF
∴△AEG∽△ABF,∴![]() =
= ![]()
∵AB=2OB,∴![]() =
= ![]() ,即
,即 ![]() =
= ![]()
∴EC=2EG,∴EG=GC
(3)延长CO交⊙O于K,连接HK
则∠K=∠CAF,∠K+∠OCH=90°
∵∠OCF=90°,∴∠HCF+∠OCH=90°
∴∠CAF=∠HCF
又∠AFC=∠CFH,∴△ACF∽△CHF,∴![]() =
= ![]()
∵cos∠AOC= ![]() ,OC=9,∴
,OC=9,∴![]() =
= ![]() =
= ![]()
∴OE=6,∴AE=3,EC 2=OC 2-OE 2=45
∴AC= ![]() =3
=3![]()
∵![]() =
= ![]() ,∴
,∴![]() =
= ![]() ,∴BF=9
,∴BF=9![]()
∴AF= ![]() =27
=27
∵BF、CF都是⊙O的切线,∴CF=BF=9![]()
∴![]() =
= ![]() ,∴CH=
,∴CH=![]()


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A.对角线相等的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线互相平分的四边形不一定是平行四边形
D.对角线互相垂直平分且相等的四边形一定是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接“劳动周”的到来,某校将九(1)班50名学生本周的课后劳动时间比上周都延长了10分钟,则该班学生本周劳动时间的下列数据与上周比较不发生变化的是( )
A. 平均数 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
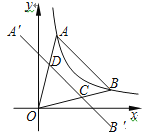
【题目】如图,点A,B在反比例函数y=![]() (x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为
(x >0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′ 分别交OA,OB于点D,C,若四边形ABCD的面积为![]() ,则点A的坐标为_______.
,则点A的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= ![]() BD;
BD;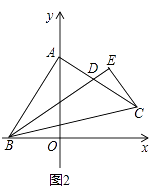
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.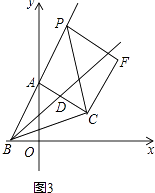
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“m=﹣1”是“直线l1:mx+(2m﹣1)y+1=0与直线l2:3x+my+3=0垂直”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com