
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,P(a,b)是△ABC的边AC上一点:
,P(a,b)是△ABC的边AC上一点:
(1)将![]() 绕原点
绕原点![]() 逆时针旋转90°得到
逆时针旋转90°得到![]() ,请在网格中画出
,请在网格中画出![]() ,旋转过程中点A所走的路径长为 .
,旋转过程中点A所走的路径长为 .
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2,并写出点A2、的坐标:A2( ).
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为 (直接写出结果).

【答案】(1)画图见解析, ![]() π ;(2)画图见解析,(4,4);(3)P3 (2a,2b)或P3 (-2a,-2b)
π ;(2)画图见解析,(4,4);(3)P3 (2a,2b)或P3 (-2a,-2b)
【解析】(1)分别得出△ABC绕点O逆时针旋转90后的对应点得到![]() 的位置,进而得到旋转后的得到
的位置,进而得到旋转后的得到![]() ,而点A所走的路径长为以O为圆心,以OA长为半径且圆心角为90°的扇形弧长;(2)由点P的对应点为P2(a+6,b+2)可知△ABC向右平移6个单位长度,再向上平移2个单位长度,即可得到的△A2B2C2;(3)以位似比2:1作图即可,注意有两个图形,与点P对应的点P3的坐标是由P的横、纵坐标都乘以2或-2得到的.
,而点A所走的路径长为以O为圆心,以OA长为半径且圆心角为90°的扇形弧长;(2)由点P的对应点为P2(a+6,b+2)可知△ABC向右平移6个单位长度,再向上平移2个单位长度,即可得到的△A2B2C2;(3)以位似比2:1作图即可,注意有两个图形,与点P对应的点P3的坐标是由P的横、纵坐标都乘以2或-2得到的.
解:(1)![]() 如图所示,
如图所示,
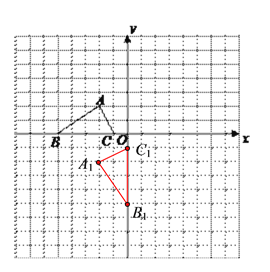
∵![]()
∴点A所走的路径长为: ![]()
故答案为: ![]() π
π
(2)∵由点P的对应点为P2(a+6,b+2)
∴△A2B2C2是△ABC向右平移6个单位长度,再向上平移2个单位长度可得到的,
∴点A对应点A2坐标为(4,4)
△A2B2C2如图所示,
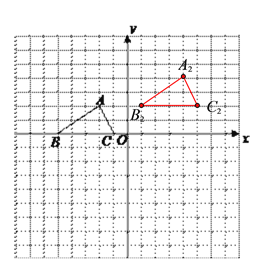
(3)∵P(a,b)且以点O为位似中心,△A3B3C3与△ABC的位似比为2:1
∴P3 (2a,2b)或P3 (-2a,-2b)
△A3B3C3如图所示,



科目:初中数学 来源: 题型:
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
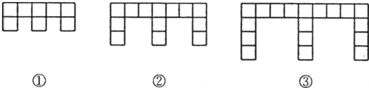
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为P,与y轴交于点A,与直线OP交于点B.
的顶点为P,与y轴交于点A,与直线OP交于点B.
(1)如图1,若点P的横坐标为1,点![]() ,
, ![]() ,试确定抛物线的解析式;
,试确定抛物线的解析式;
(2)在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM=3,求点M的坐标;
(3)如图2,若P在第一象限,且![]() ,过点P作
,过点P作![]() 轴于点D,将抛物线
轴于点D,将抛物线![]() 平移,平移后的抛物线经过点A、D,该抛物线与
平移,平移后的抛物线经过点A、D,该抛物线与![]() 轴的另一个交点为C,请探索四边形OABC的形状,并说明理由.
轴的另一个交点为C,请探索四边形OABC的形状,并说明理由.

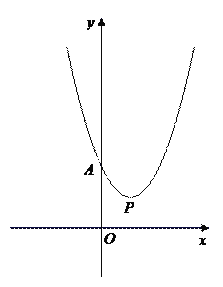
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
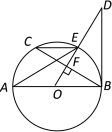
【题目】如图,AB是⊙O直径,OD⊥弦BC与点F,且交⊙O于点E,且∠AEC=∠ODB.
(1)判断直线BD和⊙O的位置关系,并给出证明;
(2)当tan∠AEC=![]() ,BC=8时,求OD的长.
,BC=8时,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
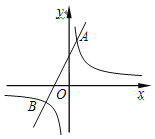
【题目】已知一次函数y1=2x+m的图象与反比例函数y2=![]() 的图象交于A,B两点,且点A的横坐标为1.
的图象交于A,B两点,且点A的横坐标为1.
(1)求一次函数的表达式;
(2)若反比例函数在第一象限的图象上有一点C到y轴的距离为3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
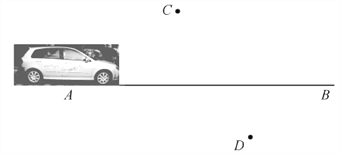
【题目】如图所示,一辆汽车在直线形的公路AB上由A向B行驶,C,D分别是位于公路AB两侧的村庄.
(1)该汽车行驶到公路AB上的某一位置C′时距离村庄C最近,行驶到D′位置时,距离村庄D最近,请在公路AB上作出C′,D′的位置(保留作图痕迹);
(2)当汽车从A出发向B行驶时,在哪一段路上距离村庄C越来越远,而离村庄D越来越近?(只叙述结论,不必说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com