
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)首先利用反比例函数图象上点的坐标性质得出k的值,再得出A、D点坐标,进而求出a,b的值;
(2)设A点的坐标为:(m, ![]() ),则C点的坐标为:(m,0),得出tan∠ADF=
),则C点的坐标为:(m,0),得出tan∠ADF= ,tan∠AEC=
,tan∠AEC=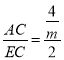 ,进而求出m的值,即可得出答案.
,进而求出m的值,即可得出答案.
试题解析:(1)∵点B(2,2)在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4,则y=![]() ,
,
∵BD⊥y轴,∴D点的坐标为:(0,2),OD=2,
∵AC⊥x轴,AC=![]() OD,∴AC=3,即A点的纵坐标为:3,
OD,∴AC=3,即A点的纵坐标为:3,
∵点A在y=![]() 的图象上,∴A点的坐标为:(
的图象上,∴A点的坐标为:(![]() ,3),
,3),
∵一次函数y=ax+b的图象经过点A、D,
∴ ,
,
解得: ![]() ,b=2;
,b=2;
(2)设A点的坐标为:(m, ![]() ),则C点的坐标为:(m,0),
),则C点的坐标为:(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=2,
∵BD∥CE,∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF= ,
,
在Rt△ACE中,tan∠AEC=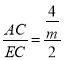 ,
,
∴![]() =
=![]() ,
,
解得:m=1,
∴C点的坐标为:(1,0),则BC=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
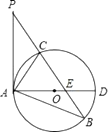
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=12,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
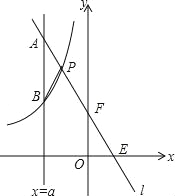
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
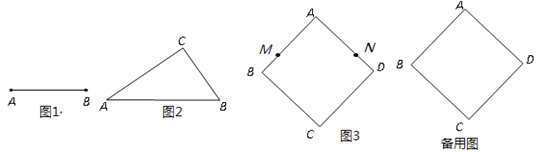
【题目】如果一个三角形有一边上的中线与这边的长相等,那么称这个三角形为“和谐三角形”.
(1)请用直尺和圆规在图1中画一个以线段AB为一边的“和谐三角形”;
(2)如图2,在△ABC中,∠C=90°,AB=![]() ,BC=
,BC=![]() ,请你判断△ABC是否是“和谐三角形”?证明你的结论;
,请你判断△ABC是否是“和谐三角形”?证明你的结论;
(3)如图3,已知正方形ABCD的边长为1,动点M,N从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点M经过的路程为S,当△AMN为“和谐三角形”时,求S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com