
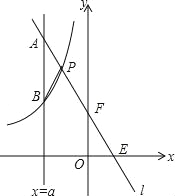
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
【答案】(1)y=﹣2x+2;(2)a=-2.
【解析】
试题分析:(1)先由y=![]() ,求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
,求出点P的坐标,再根据F为PE中点,求出F的坐标,把P,F的坐标代入求出直线l的解析式;
(2)过P作PD⊥AB,垂足为点D,由A点的纵坐标为﹣2a+2,B点的纵坐标为![]() ,D点的纵坐标为4,列出方程求解即可.
,D点的纵坐标为4,列出方程求解即可.
试题解析:(1)由P(﹣1,n)在y=![]() 上,得n=4,
上,得n=4,
∴P(﹣1,4),
∵F为PE中点,
∴OF=![]() n=2,
n=2,
∴F(0,2),
又∵P,F在y=kx+b上,
∴![]() ,解得
,解得![]() .
.
∴直线l的解析式为:y=﹣2x+2.
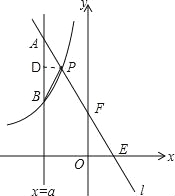
(2)如图,过P作PD⊥AB,垂足为点D,
∵PA=PB,
∴点D为AB的中点,
又由题意知A点的纵坐标为﹣2a+2,B点的纵坐标为![]() ,D点的纵坐标为4,
,D点的纵坐标为4,
∴得方程﹣2a+2![]() =4×2,
=4×2,
解得![]() =﹣2,
=﹣2,![]() =﹣1(舍去).
=﹣1(舍去).
∴当a=﹣2时,PA=PB.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了奖励在数学竞赛中获奖的学生,买了若干本课外读物准备送给他们,如果每人送3本,则还余8本;如果前面每人送5本,则最后一人得到的课外读物不足3本,设该校买了m本课外读物,有x名学生获奖,请解答下列问题:
(1)用含x的代数式表示m;
(2)求出该校的获奖人数及所买课外读物的本数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价为50元,连续两次涨价x%后售价为60元,则下面所列方程正确的是( )
A.50(1+x)2=60B.50(1+x%)2=60
C.(50+x%)2=60D.50(1+2x2)=60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点. 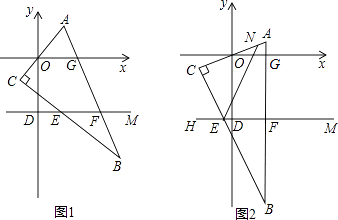
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系: .
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
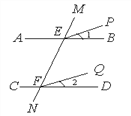
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国移动近日推出“4G商旅套餐”,其中![]() 两种计费方法如下:
两种计费方法如下:
计费 | 月租费 | 国内主叫 | 国内主叫 | 备注 |
A | 58 |
| 150 | 全国范围内接听免费,含来电显示 |
B | 88 | 350 |
![]() 说明:
说明:![]() 指在国内任何地方拨打任何电话的资费;
指在国内任何地方拨打任何电话的资费;![]() 指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元
指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元![]() 月;若主叫时间为200分钟,则计费为
月;若主叫时间为200分钟,则计费为![]() 元
元![]()
![]() 在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
![]() 若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
![]() 经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com