
【题目】中国移动近日推出“4G商旅套餐”,其中![]() 两种计费方法如下:
两种计费方法如下:
计费 | 月租费 | 国内主叫 | 国内主叫 | 备注 |
A | 58 |
| 150 | 全国范围内接听免费,含来电显示 |
B | 88 | 350 |
![]() 说明:
说明:![]() 指在国内任何地方拨打任何电话的资费;
指在国内任何地方拨打任何电话的资费;![]() 指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元
指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元![]() 月;若主叫时间为200分钟,则计费为
月;若主叫时间为200分钟,则计费为![]() 元
元![]()
![]() 在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
![]() 若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
![]() 经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
【答案】(1) 88元,97.5元;(2)见解析;(3)该用户的选择不合理
【解析】试题分析(1)根据B种计费方法,求出费用即可.
(2)用分段函数表示两种收费方式即可.
(3)先求出国内主叫时间,再求出选择B的费用,比较即可判断.
试题解析:(1)在B种计费方法中,若某用户在该月主叫时间为170分钟,费用为88元.
400分钟的费用为88+0.19×(400-350)=97.5元.
(2)yA=![]() ,yB=
,yB=![]() .
.
(3)设国内主叫时间为x分钟.
由题意58+0.19(x-150)=115,
解得x=450,
如果选择B费用为88+0.19(450-350)=107元,
107<115,
该用户的选择不合理.


科目:初中数学 来源: 题型:
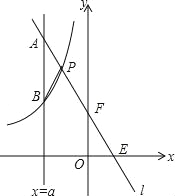
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=![]() (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.
(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形有一边上的中线与这边的长相等,那么称这个三角形为“和谐三角形”.
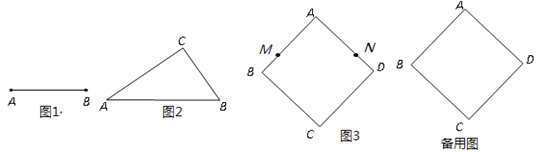
(1)请用直尺和圆规在图1中画一个以线段AB为一边的“和谐三角形”;
(2)如图2,在△ABC中,∠C=90°,AB=![]() ,BC=
,BC=![]() ,请你判断△ABC是否是“和谐三角形”?证明你的结论;
,请你判断△ABC是否是“和谐三角形”?证明你的结论;
(3)如图3,已知正方形ABCD的边长为1,动点M,N从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点M经过的路程为S,当△AMN为“和谐三角形”时,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售甲、乙两种糖果,购买3千克甲种糖果和1千克乙种糖果共需44元,购买1千克甲种糖果和2千克乙种糖果共需38元.
(1)求甲、乙两种糖果的价格;
(2)若购买甲、乙两种糖果共20千克,且总价不超过240元,问甲种糖果最少购买多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣5,3)、B(﹣2,﹣2)、C(﹣3,4). 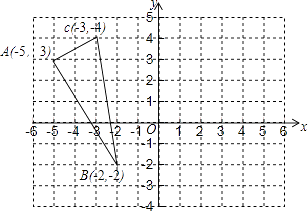
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)写出点A关于x轴对称的点A2的坐标;
(3)△ABC的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com