
【题目】如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE,若点A到CE的距离为17,则CE=_____.
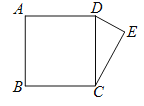
【答案】12或5
【解析】分两种情况:
①如图,连接AC,过点A作AF⊥EC于点F,即可得AF=17,由正方形ABCD的边长为13,根据勾股定理可求得AC=![]() ,在Rt△ACF中,根据勾股定理求得FC=7,易证△ADM∽△CFM,根据相似三角形的性质可得
,在Rt△ACF中,根据勾股定理求得FC=7,易证△ADM∽△CFM,根据相似三角形的性质可得![]() ,设CM=x,FM=y,即可得
,设CM=x,FM=y,即可得![]() ,所以可得
,所以可得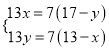 ,解得
,解得 ,又由
,又由![]() 可得
可得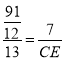 ,解得CE=12 ;
,解得CE=12 ;

②如图,连接AC,过点A作AF⊥EC交EC的延长线于点F,即可得AF=17,由正方形ABCD的边长为13,根据勾股定理可求得AC=![]() ,在Rt△ACF中,根据勾股定理求得FC=7,易证△ABM∽△CFM,根据相似三角形的性质可得
,在Rt△ACF中,根据勾股定理求得FC=7,易证△ABM∽△CFM,根据相似三角形的性质可得![]() ,设CM=x,FM=y,即可得
,设CM=x,FM=y,即可得![]() ,所以可得
,所以可得 ,解得
,解得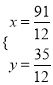 ,易证△FCM∽△EDC,根据相似三角形的性质可得
,易证△FCM∽△EDC,根据相似三角形的性质可得![]() 可得
可得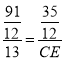 ,解得CE=5.
,解得CE=5.


科目:初中数学 来源: 题型:
【题目】中国移动近日推出“4G商旅套餐”,其中![]() 两种计费方法如下:
两种计费方法如下:
计费 | 月租费 | 国内主叫 | 国内主叫 | 备注 |
A | 58 |
| 150 | 全国范围内接听免费,含来电显示 |
B | 88 | 350 |
![]() 说明:
说明:![]() 指在国内任何地方拨打任何电话的资费;
指在国内任何地方拨打任何电话的资费;![]() 指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元
指在国内任何地方拨打任何电话的通话时限,如A计费方法中,若主叫时间小于等于150分钟,则只收月租费58元![]() 月;若主叫时间为200分钟,则计费为
月;若主叫时间为200分钟,则计费为![]() 元
元![]()
![]() 在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
在B种计费方法中,若某用户在该月主叫时间为170分钟,则该用户的月缴费为多少元?400分钟呢?
![]() 若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
若选择A计费方法,设某用户一个月的国内主叫时间为x,试用含x的代数式表示该用户的月话费;若选择B计费方法呢?
![]() 经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
经过统计,选择计费方法A的某用户一个月所需的平均话费为115元,你觉得该用户的选择合理吗?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
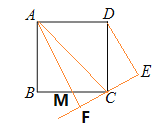
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
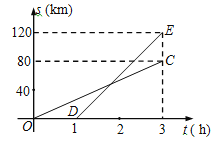
A. 乙到达B地时甲距A地120km. B. 乙出发1.8小时被甲追上.
C. 甲,乙相距20km时,t为2.4h. D. 甲的速度是乙的速度的![]() 倍.
倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“抢红包”是2015年春节十分火爆的一项网络活动,某企业有4000名职工,从中随机抽取350人,按年龄分布和“抢红包”所持态度情况进行调查,并将调查结果绘成了条形统计图和扇形统计图.
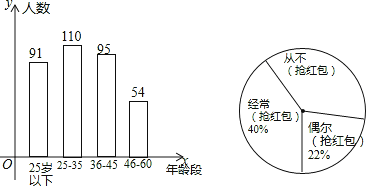
(1)这次调查中,如果职工年龄的中位数是整数,那么这个中位数所在的年龄段是哪一段?
(2)如果把对“抢红包”所持态度中的“经常(抢红包)”和“偶尔(抢红包)”统称为“参与抢红包”,那么这次接受调查的职工中“参与抢红包”的人数是多少?并估计该企业“从不(抢红包)”的人数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com