
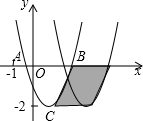
 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )| A. | b>0 | B. | a-b+c<0 | ||
| C. | 阴影部分的面积为4 | D. | 若c=1,则b2=-4a |
分析 根据抛物线开口向上,可得a>0;然后根据对称轴为x=-$\frac{b}{2a}$>0,可得b<0,据此判断A.
根据抛物线y=ax2+bx+c的图象,可得x=-1时,y>0,即a-b+c>0,据此判断B.
根据阴影部分是一个平行四边形,然后根据平行四边形的面积=底×高,求出阴影部分的面积是多少即可判断C.
根据函数的最小值是$\frac{4ac-{b}^{2}}{4a}$=-2,得出c=-1时,a、b的关系即可判断D.
解答 解:∵抛物线开口向上,
∴a>0,
又∵对称轴为x=-$\frac{b}{2a}$>0,
∴b<0,故A不正确;
∵x=-1时,y>0,
∴a-b+c>0,故B不正确;
∵抛物线向右平移了2个单位,
∴平行四边形的底是2,
∵函数y=ax2+bx+c的最小值是y=-2,
∴平行四边形的高是2,
∴阴影部分的面积是:2×2=4,故C正确;
∵$\frac{4ac-{b}^{2}}{4a}$=-2,c=-1,
∴b2=4a,故D不正确.
故选C.
点评 此题主要考查了二次函数的图象与几何变换,二次函数的图象与系数的关系,熟练掌握平移的规律和二次函数的性质,解答此类问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,点O在AB上,⊙O经过B,D两点,交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
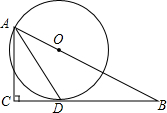 如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
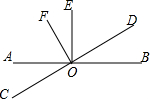 如图,已知∠AOB、∠COD都为平角,∠AOE、∠BOE、∠COF、∠DOF都等于90°.
如图,已知∠AOB、∠COD都为平角,∠AOE、∠BOE、∠COF、∠DOF都等于90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com