
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:选择题
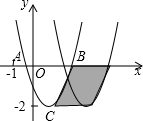 如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )
如图,已知抛物线y=ax2+bx+c与x轴交于A,B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是( )| A. | b>0 | B. | a-b+c<0 | ||
| C. | 阴影部分的面积为4 | D. | 若c=1,则b2=-4a |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
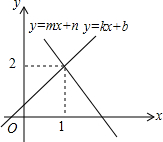 如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
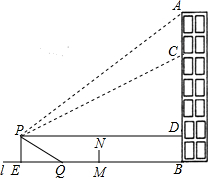 如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.
如图,重庆某广场新建的与建筑物AB垂直的空中玻璃走廊PD与AB相连,AB与地面l垂直,在P处测得建筑物顶端A的仰角为36°,在建筑物上的C处测得P处的俯角为30°(不计测量人员的身高),测得CD为30米,图中的点A、B、C、D、P及直线l均在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. | 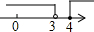 | D. | 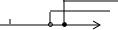 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
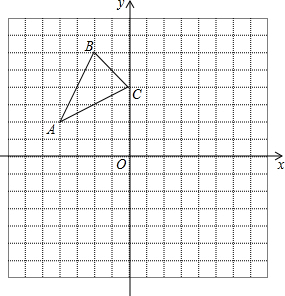 如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.
如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系平面上三点.查看答案和解析>>
科目:初中数学 来源:2017届广东省南雄市九年级下学期模拟考试数学试卷(解析版) 题型:判断题
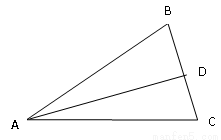
已知:如图,在△ABC中,AD平分∠ABC.
(1)做线段AD的垂直平分线MN,MN与AB边交于点E,AC边交于点F。
(2)若AB=AC,请直接写出EF和BC的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com