
分析 (1)先化简各二次根式,再合并括号内同类二次根式和计算除法,最后计算乘法可得;
(2)先将括号内分式通分后相加同时将除法转化为乘法,再约分即可化简分式,将a的值代入计算即可.
解答 解:(1)原式=$2\sqrt{3}$(2$\sqrt{3}$-5$\sqrt{3}$)+2$\sqrt{3}$$÷2\sqrt{3}$
=2$\sqrt{3}$×$(-3\sqrt{3})$+1
=-18+1
=-17;
(2)原式=$\frac{{a}^{2}-1+2}{a+1}•\frac{1}{{a}^{2}+1}$
=$\frac{{a}^{2}+1}{a+1}•\frac{1}{{a}^{2}+1}$
=$\frac{1}{a+1}$,
当a=$\sqrt{2}-1$时,
原式=$\frac{1}{\sqrt{2}+1-1}$=$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
点评 本题主要考查二次根式的混合运算和分式的化简求值,熟练掌握它们的运算顺序和运算法则是解题的关键和根本.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
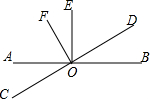 如图,已知∠AOB、∠COD都为平角,∠AOE、∠BOE、∠COF、∠DOF都等于90°.
如图,已知∠AOB、∠COD都为平角,∠AOE、∠BOE、∠COF、∠DOF都等于90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.5×106m3 | B. | 9.5×107m3 | C. | 9.5×108m3 | D. | 9.5×109m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com