
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
科目:初中数学 来源: 题型:选择题
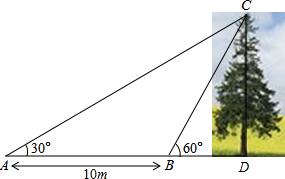 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 所有等腰直角三角形都相似 | |
| B. | 两边对应相等的两个直角三角形全等 | |
| C. | 圆中垂直于弦的直径平分这条弦 | |
| D. | 顺次连接对角线相等的四边形各边中点得到的四边形是矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
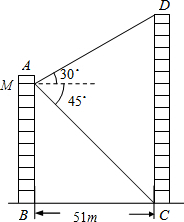 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
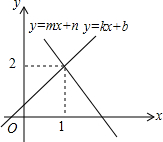 如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图所示的是函数y=kx+b与y=mx+n的图象,则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=mx+n}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.
如图,⊙O为△ABC的外接圆,AB为⊙O的直径,延长AB到点E,连结EC,且∠BCE=∠BAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com