
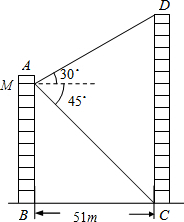
 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数) 分析 过点M作ME⊥CD于E,则四边形BCEP是矩形,得到ME=BC=30,在Rt△MDE中,利用∠DME=30°,求得DE的长;在Rt△MEC中,利用∠EMC=45°,求得CE的长,利用CD=DE﹢CE即可求得结果.
解答 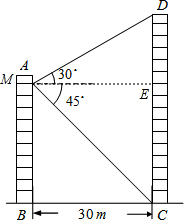 解:过点M作ME⊥CD于E,则四边形BCEM是矩形.
解:过点M作ME⊥CD于E,则四边形BCEM是矩形.
∴ME=BC=51.
在Rt△MDE中,
∵∠DME=30°,ME=30,
∴DE=ME×tan30°=51×$\frac{\sqrt{3}}{3}$=17$\sqrt{3}$.
在Rt△MEC中,∵∠EMC=45°,ME=51,
∴CE=ME×tan45°=51×1=30.
∴CD=DE﹢CE=51﹢17$\sqrt{3}$=30﹢17.3≈80(m).
答:建筑物CD的高约为80m.
点评 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
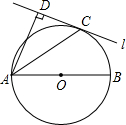 如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.
如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
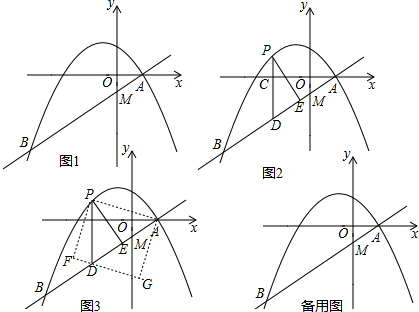
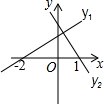 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.5×106m3 | B. | 9.5×107m3 | C. | 9.5×108m3 | D. | 9.5×109m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )
如图,抛物线y=ax2+bx+c与y轴正半轴相交,其顶点坐标为(-$\frac{1}{2}$,1),有下列结论:①ac<0;②a-b=1;③4ac<b2;④a-b+c<0,其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com