
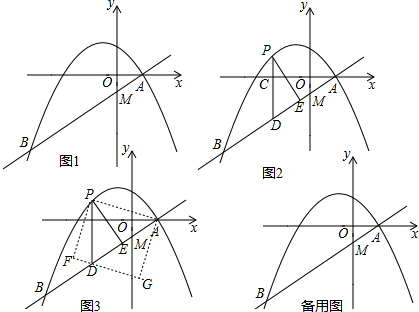
分析 (1)利用直线解析式求出点A、B的坐标,再利用待定系数法求二次函数解析式解答;
(2)①利用直线解析式和抛物线解析式表示出PD,再利用同角的余角相等求出∠DPE=∠BAO,根据直线k值求出∠BAO的正弦和余弦值,然后表示出PE、DE,再根据三角形的周长公式列式整理即可得解,再根据二次函数的最值问题解答;
②点G在y轴上时,得到△ACP≌△GOA全等,根据全等三角形对应边相等可得PC=AO=2,然后利用二次函数解析式求解即可.
解答 解:(1)对于y=$\frac{3}{4}$x-$\frac{3}{2}$,当y=0时,x=2,当x=-8时,y=-$\frac{15}{2}$,
∴A(2,0),B(-8,-$\frac{15}{2}$),
∵A,B在抛物线y=-$\frac{1}{4}$x2+bx+c,
∴0=-1+2b+c,-$\frac{15}{2}$=-16-8b+c,
∴b=-$\frac{3}{4}$,c=$\frac{5}{2}$.
∴y=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$.
(2)①设直线y=$\frac{3}{4}$x-$\frac{3}{2}$与y轴交于点M,
∴M(0,-$\frac{3}{2}$),
∴OM=$\frac{3}{2}$,
∵A(2,0),
∴OA=2,
∴AM=$\sqrt{{OA}^{2}{+OM}^{2}}$=$\frac{5}{2}$,
∴OM:OA:AM=3:4:5,
由题意有:∠PDE=∠OMA,∠AOM=PED=90°,
∴△AOM∽△PED,
∴DE:PE:PD=3:4:5,
∵点P是直线AB上方的抛物线上一动点,
∴PD=yP-yD=(-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$)-($\frac{3}{4}$x-$\frac{3}{2}$)=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4.
∴DE=$\frac{3}{5}$(-$\frac{1}{4}$x2-$\frac{3}{2}$x+4).PE=$\frac{4}{5}$(-$\frac{1}{4}$x2-$\frac{3}{2}$x+4)
∴l=DE+PE+PD=$\frac{3}{5}$(-$\frac{1}{4}$x2-$\frac{3}{2}$x+4)+$\frac{4}{5}$(-$\frac{1}{4}$x2-$\frac{3}{2}$x+4)+(-$\frac{1}{4}$x2-$\frac{3}{2}$x+4).
=-$\frac{3}{5}$(x+3)2+15.
∴当x=-3时,l最大=15.
∵点P在直线AB上方的抛物线上,
∴-8<x<2
故答案为-8<x<2.
②满足题意的点有三个,分别为P1($\frac{-3+\sqrt{17}}{2}$,2),P2($\frac{-3-\sqrt{17}}{2}$),P3($\frac{-7+\sqrt{89}}{2}$,$\frac{-7+\sqrt{89}}{2}$),
(Ⅰ)当点G落在y轴上时,△ACP≌△GOA,
∴PC=AO=2,
∴-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$=2.
∴x=$\frac{-3±\sqrt{17}}{2}$,
∴P1($\frac{-3+\sqrt{17}}{2}$,2),P2($\frac{-3-\sqrt{17}}{2}$).
(Ⅱ)当点F落在y轴上时,同法可得:P3($\frac{-7+\sqrt{89}}{2}$,$\frac{-7+\sqrt{89}}{2}$),P4($\frac{-7-\sqrt{89}}{2}$,$\frac{-7-\sqrt{89}}{2}$)(舍)
∴满足题意的点有三个,分别为P1($\frac{-3+\sqrt{17}}{2}$,2),P2($\frac{-3-\sqrt{17}}{2}$),P3($\frac{-7+\sqrt{89}}{2}$,$\frac{-7+\sqrt{89}}{2}$),
点评 此题主要考查了二次函数的综合应用,全等三角形的判定与性质以及待定系数法求二次函数解析式,锐角三角函数的应用,(1)①利用锐角三角函数用PD表示出三角形是周长是解题的关键,②难点在于分情况讨论.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
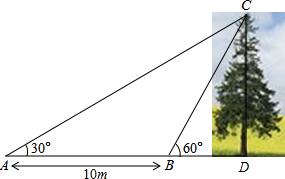 如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )
如图,某教学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )| A. | 10m | B. | 5m | C. | 5$\sqrt{3}$m | D. | 10$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
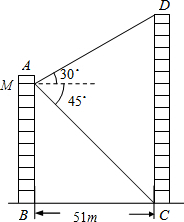 如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)
如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.($\sqrt{3}$取1.73,结果保留整数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com