
分析 (1)根据题意先画出树状图,得出一共有12种情况,两个小球的颜色恰好能配成紫色的有8种情况,即可求出甲获胜的概率;
(2)求出乙获胜的概率,再与甲比较即可.
解答 解:(1)由题意,列表格得:
| 甲 乙 | 红1 | 红2 | 蓝1 | 蓝2 |
| 红1 | (红,红) | (蓝,红) | (蓝,红) | |
| 红2 | (红,红) | (蓝,红) | (蓝,红) | |
| 蓝1 | (红,蓝) | (红,蓝) | (蓝,蓝) | |
| 蓝2 | (红,蓝) | (红,蓝) | (蓝,蓝) |
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个人取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
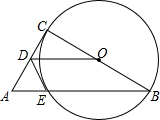 如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.
如图,在Rt△ABC中,∠ACB=90°,以BC为直径画⊙O,交斜边AB于点E,点D为AC中点,连接OD,DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
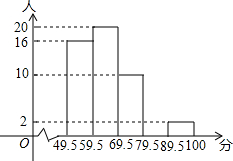 某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:
某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
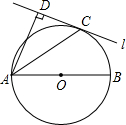 如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.
如图,AB为⊙O的直径,AC为弦,过C点的直线为l,AD⊥l于D,又AC平分∠DAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com