
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
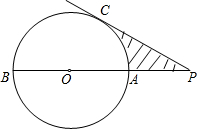 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
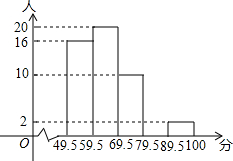 某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:
某校七年级有200名学生参加了全国中小学生安全知识竞赛初赛,为了了解本校初赛的成绩情况,从中抽取了50名学校,将他们的初赛成绩(得分为整数,满分100分)分成五组:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
如图,在每个小正方形边长为1的网格纸中,将格点△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
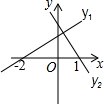 如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )
如图是一次函数y1=ax+b,y2=cx+d的图象,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$解集是( )| A. | x<-2 | B. | -2<x<1 | C. | x>0 | D. | x>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com