
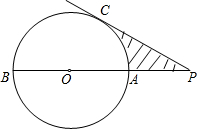
 如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
如图,已知AB是⊙O的直径,P为BA延长线上一点,PC切⊙O于C,若⊙O的半径是4cm,∠P=30°,图中阴影部分的面积是8$\sqrt{3}$-$\frac{8}{3}π$(cm2). 分析 利用扇形的面积公式,以及阴影部分的面积=S△OCP-S扇形OCA即可求解.
解答 解:∵⊙O的半径是4cm,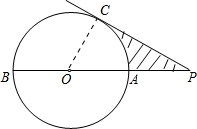
∴AB=8cm,
则OC=$\frac{1}{2}$AB=4cm,
∵直角△OCP中,∠P=30°,
∴OP=2OC=8,
∴CP=$\sqrt{O{P}^{2}-O{C}^{2}}=4\sqrt{3}$,
∴S△OCP=$\frac{1}{2}$OC•CP=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$(cm2),
S扇形OCA=$\frac{60π×{4}^{2}}{360}$=$\frac{8}{3}π$(cm2),
则阴影部分的面积=8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
故答案为:8$\sqrt{3}$-$\frac{8}{3}π$(cm2).
点评 本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
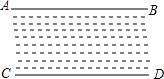 如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.
如图所示,直线AB,CD表示一条小河的两条河岸线,小明和小刚想利用数学知识判断这里两条河岸线是否平行,两人现在分别在小河的两侧,每人手中各有两根标杆和一个测角仪,请你帮他们想象办法.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )
如图,PA、PB是⊙O的切线,点A和B是切点,AC是⊙O的直径,已知∠P=5O°,则∠ACB的大小是( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
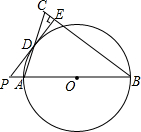 如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.
如图,在以△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过点D作PE⊥BC交BC于点E,交AB的延长线于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
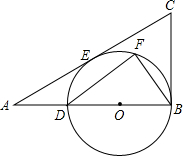 如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.
如图,在Rt△ABC中,∠B=90°,tanA=$\frac{3}{4}$,点D在边AB上,AD=4,以BD为直径的⊙O与边AC切于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com