Question

1．如图，在平面直角坐标系中放入一张矩形纸片ABCD，将纸片翻转后，点B恰好落在x轴上的B′处，折痕CE所在的直线与x轴的交点为F，已知OC：OB′=3：4．

（1）如果OC=9，求此时点E的坐标；
（2）如果OC=x，△AEF的面积为y，求y关于x的函数解析式，及自变量x的取值范围；
（3）如果△AEF的面积为$\frac{32}{3}$时，求折痕CE所在直线的函数解析式．

Answer 1

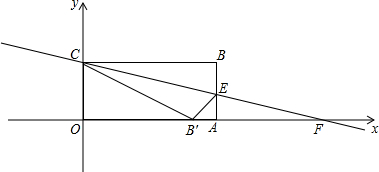
分析 （1）根据比的性质，可得OB′的长根据折叠的性质，可得BC，BE的长，根据勾股定理，可得AE的长，可得E点的坐标；
（2）根据比的性质，可得OB′的长根据折叠的性质，可得BC，BE的长，根据勾股定理，可得AE的长，可得E点的坐标，根据待定系数法，可得CE的解析式，根据自变量与函数值的关系，可得F点坐标，根据三角形的面积公式可得函数解析式；
（3）根据函数值，可得相应自变量的值，可得CE的解析式．

解答 解：（1）由OC：OB′=3：4，OC=9，得
OB′=12．
由勾股定理，得
CB′=$\sqrt{O{C}^{2}+B′{O}^{2}}$=$\sqrt{{9}^{2}+1{2}^{2}}$=15．
由折叠的性质，得BC=CB′=15，BE=B′E．
由矩形的性质，得AO=BC=15，AB=OC=9．
设AE=x，BE=B′E=（9-x），AB′=AO-OB′=15-12=3，
由勾股定理，得
AB′²+AE²=B′E²，即
3²+x²=（9-x）²．
解得x=4，
E点坐标是（15，4）；
（2）设OC=AB=c，AE=e，由OC：OB′=3：4，得
OB′=$\frac{4}{3}$c，CB′=$\sqrt{{c}^{2}+（\frac{4}{3}c）^{2}}$=$\frac{5}{3}$c，
CB=CB′=OA=$\frac{5}{3}$c．
AB′=AO-OB′=$\frac{5}{3}$c-$\frac{4}{3}$c=$\frac{c}{3}$．
BE=B′E=AB-AE=c-e．
由勾股定理，得
（c-e）²=b²+（$\frac{c}{3}$）²．
解得e=$\frac{4}{9}$c，即E（$\frac{5}{3}$c，$\frac{4}{9}$c）．
设CE的解析式为y=kx+b，
将C、E点坐标代入函数解析式，得
$\left\{\begin{array}{l}{\frac{5}{3}ck+b=\frac{4}{9}c}\\{b=c}\end{array}\right.$．
解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=c}\end{array}\right.$
CE的解析式为y=-$\frac{1}{3}$x+c．
当y=0时，-$\frac{1}{3}$x+c=0．解得x=3c．
F点的坐标是（3c，0）
FA=OF-OA=3c-$\frac{5}{3}$c=$\frac{4}{3}$c．
当c=x时，y=$\frac{1}{2}$•AF•AE=$\frac{1}{2}$×$\frac{4}{3}$x×$\frac{4}{9}$x，
即y=$\frac{8}{27}$x²  （x＞0）；
（3）当y=$\frac{32}{3}$时，$\frac{8}{27}$x²=$\frac{32}{3}$．
解得x=6，x=-6不符合题意（舍），
CE的函数解析式为y=-$\frac{1}{3}$x+6．

点评 本题考查了一次函数综合题，利用了比例的性质，折叠的性质，勾股定理，待定系数法求函数解析式，三角形的面积公式，在Rt△ABE′利用勾股定理是解题关键．