
 阅读理解题
阅读理解题分析 (1)根据第一个数表示左右方向,第二个数表示上下方向结合图形写出即可;
(2)根据行走路线列出算式计算即可得解;
(3)根据方格和标记方法作出线路图即可得解.
解答 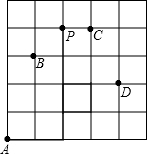 解:(1)∵规定:向上向右走为正,向下向左走为负,
解:(1)∵规定:向上向右走为正,向下向左走为负,
∴A→C(3,3),C→B记为(-2,-1).
故答案为3,3,B,-1;
(2)据已知条件可知:A→B:(1,3),B→C(2,1),C→D(1,-2),该甲虫走过的路线长为1+3+2+1+1+2=10.
(3)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+1,-1),(-1,+3),P点位置如图所示.
点评 本题考查了坐标确定位置,正数和负数,读懂题目信息,理解行走路线的记录方法是解题的关键.


科目:初中数学 来源: 题型:解答题
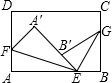 如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?
如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化/万人 | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | -0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com