
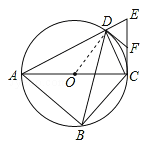
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.

(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
【答案】(1)90°;(2)详见解析;(3)2.
【解析】
试题分析:(1)根据圆周角定理即可得∠CDE的度数;(2)连接DO,根据直角三角形的性质和等腰三角形的性质易证∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,即可判定DF是⊙O的切线;(3)根据已知条件易证△CDE∽△ADC,利用相似三角形的性质结合勾股定理表示出AD,DC的长,再利用圆周角定理得出tan∠ABD的值即可.
试题解析:(1)解:∵对角线AC为⊙O的直径,
∴∠ADC=90°,
∴∠EDC=90°;
(2)证明:连接DO,
∵∠EDC=90°,F是EC的中点,
∴DF=FC,
∴∠FDC=∠FCD,
∵OD=OC,
∴∠OCD=∠ODC,
∵∠OCF=90°,
∴∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,
∴DF是⊙O的切线;
(3)解:如图所示:可得∠ABD=∠ACD,
∵∠E+∠DCE=90°,∠DCA+∠DCE=90°,
∴∠DCA=∠E,
又∵∠ADC=∠CDE=90°,
∴△CDE∽△ADC,
∴![]() =
=![]() ,
,
∴DC2=ADDE
∵AC=2![]() DE,
DE,
∴设DE=x,则AC=2![]() x,
x,
则AC2﹣AD2=ADDE,
期(2![]() x)2﹣AD2=ADx,
x)2﹣AD2=ADx,
整理得:AD2+ADx﹣20x2=0,
解得:AD=4x或﹣4.5x(负数舍去),
则DC=![]() =2x,
=2x,
故tan∠ABD=tan∠ACD=![]() =
=![]() =2.
=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B型台灯共需470元.
(1)求A、B两种型号台灯每台分别多少元?
(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数![]() 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题:
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若S△BOD=4,请回答下列问题:
(1)求反比例函数解析式;
(2)求C点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形ABC中,∠C=90°,将△ABC绕点A逆时针旋转至△AED,使点C的对应点D恰好落在边AB上,E为点B的对应点.设∠BAC=α,则∠BED=______.(用含α的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一副三角板的直角重合放置,其中∠A=30°,∠CDE=45°.
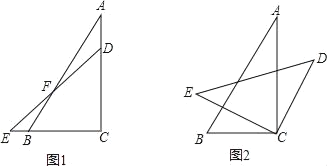
(1)如图1,求∠EFB的度数;
(2)若三角板ACB的位置保持不动,将三角板CDE绕其直角顶点C顺时针方向旋转.
①当旋转至如图2所示位置时,恰好CD∥AB,则∠ECB的度数为 ;
②若将三角板CDE继续绕点C旋转,直至回到图1位置.在这一过程中,是否还会存在△CDE其中一边与AB平行?如果存在,请你画出示意图,并直接写出相应的∠ECB的大小;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
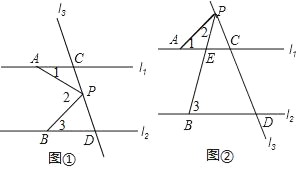
【题目】如图①,已知直线l1、l2,直线l3和直线l1、l2交于点C和D,在直线l3上有动点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上.
(1)如果点P在C、D之间运动时,且满足∠1+∠3=∠2,请写出l1与l2之间的位置关系 ;
(2)如图②如果l1∥l2,点P在直线l1的上方运动时,试猜想∠1+∠2与∠3之间关系并给予证明;
(3)如果l1∥l2,点P在直线l2的下方运动时,请直接写出∠PAC、∠PBD、∠APB之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
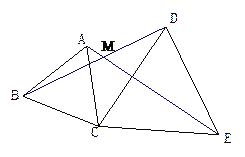
【题目】如图,把△ACE绕点C逆时针旋转60°后与△BCD重合,BD、AE.交于点 M,连接AB、DE.
(1)求证:△ABC和△CDE为等边三角形;
(2)求∠AMB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com