练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知矩形ABCD的长和宽分别为16cm和12cm，连接其对边中点，得到四个矩形，顺次连接矩形AEFG各边中点，得到菱形l1；连接矩形FMCH对边中点，又得到四个矩形，顺次连接矩形FNPQ各边中点，得到菱形l2；…如此操作下去，则l4的面积是cm2 ．

    【答案】
    【解析】解：∵矩形ABCD的长和宽分别为16cm和12cm，

    ∴EF=8cm，AE=6cm，

    ∴菱形l1的面积= ×8×6=24cm2，

    同理，菱形l2的面积= ×4×36cm2，

    则菱形l3的面积= ×2× = cm2，

    ∴菱形l4的面积= ×1× = cm2，

    所以答案是： ．


    【考点精析】关于本题考查的菱形的性质，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：用3辆A型车和2辆B型车载满货物一次可运货共19吨；用2辆A型车和3辆B型车载满货物一次可运货共21吨．

    （1）1辆A型车和1辆B型车都载满货物一次分别可以运货多少吨?

    （2）某物流公司现有49吨货物，计划同时租用A型车辆，B型车辆，一次运完，且恰好每辆车都载满货物．

    ①求、的值；

    ②若A型车每辆需租金130元/次，B型车每辆需租金200元/次．请求出租车费用最少是多少元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列不等式(组)，并把解集在数轴上表示出来：

    (1)

    (2)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△DEF中，DE＝DF，点B在EF边上，且∠EBD＝60°，C是射线BD上的一个动点(不与点B重合，且BC≠BE)，在射线BE上截取BA＝BC，连接AC．

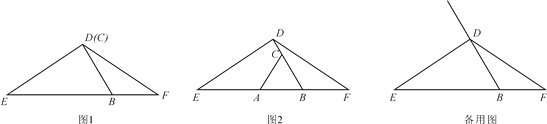
    （1）当点C在线段BD上时，

    ①若点C与点D重合，请根据题意补全图1，并直接写出线段AE与BF的数量关系为________；

    ②如图2，若点C不与点D重合，请证明AE＝BF＋CD；

    （2）当点C在线段BD的延长线上时，用等式表示线段AE，BF，CD之间的数量关系，不用证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，AB为半圆O的直径，C为圆上一点，AD平分∠BAC交半圆于点D，过点D作DE⊥AC，DE交AC的延长线于点E．

    （1）求证：DE是⊙O的切线；
    （2）若⊙O的半径为2，DE= ，求线段AC的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点C、D在线段AB上，△PCD是等边三角形，且△ACP∽△PDB，求∠APB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】列方程解应用题：

    某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按元销售时，每天可销售个；若销售单价每降低元，每天可多售出个.已知每个玩具的固定成本为元，问这种玩具的销售单价为多少元时，厂家每天可获利润元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一坐标系中，函数 和 的图像大致是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=65°∠C=45°，AD是BC边上的高，AE是∠BAC的平线，求∠DAE的度数？

    查看答案和解析>>

    同步练习册答案