
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| 2a |
| 1 |
| a |
| 4a-22 |
| 4a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| b |
| 2a |
| 4ac-b2 |
| 4a |


科目:初中数学 来源: 题型:
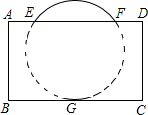 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.圆O与纸盒交于E、F、G三点,已知EF=CD=16cm.
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.圆O与纸盒交于E、F、G三点,已知EF=CD=16cm.查看答案和解析>>
科目:初中数学 来源: 题型:
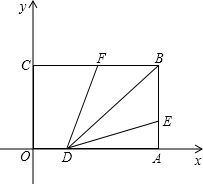 如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.
如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=
如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=| k |
| x |
| A、S是变化的,因为菱形CDEF中只有C点的位置是确定的,其它三点都不是固定的 | ||||||||||
| B、当D点从C点到B点运动时,S逐渐增大 | ||||||||||
| C、从图上看,可以用两个菱形的面积减去两个三角形的面积,但E、F两点不确定,所以还是不能求出 | ||||||||||
D、如果连接CE,则CE∥OB,△OBE与△OBC同底(OB)共高,则S△OBE=S△OBC,OC=OA=2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 7×9 |
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com